如图,平面直角坐标系xOy中,一次函数y=-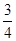 x+b(b为常数,b>0)的图象与x轴、y轴分别相交于点A、B,半径为4的⊙O与x轴正半轴相交于点C,与y轴相交于点D、E,点D在点E上方.
x+b(b为常数,b>0)的图象与x轴、y轴分别相交于点A、B,半径为4的⊙O与x轴正半轴相交于点C,与y轴相交于点D、E,点D在点E上方.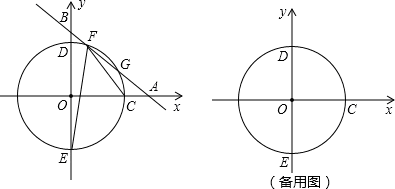
(1)若直线AB与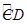 有两个交点F、G.
有两个交点F、G.
①求∠CFE的度数;
②用含b的代数式表示FG2,并直接写出b的取值范围;
(2)设b≥5,在线段AB上是否存在点P,使∠CPE=45°?若存在,请求出P点坐标;若不存在,请说明理由.
推荐套卷
如图,平面直角坐标系xOy中,一次函数y=-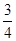 x+b(b为常数,b>0)的图象与x轴、y轴分别相交于点A、B,半径为4的⊙O与x轴正半轴相交于点C,与y轴相交于点D、E,点D在点E上方.
x+b(b为常数,b>0)的图象与x轴、y轴分别相交于点A、B,半径为4的⊙O与x轴正半轴相交于点C,与y轴相交于点D、E,点D在点E上方.
(1)若直线AB与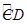 有两个交点F、G.
有两个交点F、G.
①求∠CFE的度数;
②用含b的代数式表示FG2,并直接写出b的取值范围;
(2)设b≥5,在线段AB上是否存在点P,使∠CPE=45°?若存在,请求出P点坐标;若不存在,请说明理由.