江苏省兴化市常青藤学校联盟九年级下学期第一次月度联考数学试卷
在平面直角坐标系中,点P(3,-x2-1)所在的象限是( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
如图,数轴上表示2, 的对应点分别为C,B,点C是AB的中点,则点A表示的数是( )
的对应点分别为C,B,点C是AB的中点,则点A表示的数是( )
A. |
B. |
C. |
D. |
如图所示,在 ABCD中,对角线AC,BD相交于点O,且AB≠AD, 则下列式子不正确的是( )
ABCD中,对角线AC,BD相交于点O,且AB≠AD, 则下列式子不正确的是( )
| A.AC⊥BD | B.AB=CD | C.BO=OD | D.∠BAD=∠BCD |
如图,在直角坐标系中,四边形OABC为正方形,顶点A,C在坐标轴上,以边AB为弦的⊙M与x轴相切,若点A的坐标为(0,8),则圆心M的坐标为( )
| A.(4,5) | B.(-5,4) | C.(-4,6) | D.(-4,5) |
函数y=ax2+bx+c的图象如图所示,那么关于x的一元二次方程ax2+bx+c-3=0的根的情况是( )
| A.有两个不相等的实数根 |
| B.有两个异号的实数根 |
| C.有两个相等的实数根 |
| D.没有实数根 |
如图所示,l∥m,等腰直角△ABC的直角顶点C在直线m上,若∠β=20°,则∠α的
度数为 
如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为 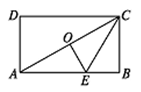
已知关于x的一次函数y=mx+n的图象如图所示,则|n-m|- 可化简为________.
可化简为________.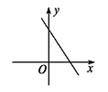
如图,△ABC中,AB=AC,点D,E分别是边AB,AC的中点,点G,F在BC边上,四边形DEFG是正方形.若DE=2 cm,则AC的长为 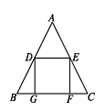
某盏路灯照射的空间可以看成如图所示的圆锥,它的高AO=8米,母线AB与底面半径OB的夹角为α,tan α= ,则此圆锥的侧面积是__________平方米(结果保留π).
,则此圆锥的侧面积是__________平方米(结果保留π).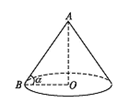
如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树
正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为2米,台阶AC的坡度为1: (即AB:AC=1:
(即AB:AC=1: ),且B,C,E三点在同一条直线上.请根据以上条件求出树DE的高度(测倾器的高度忽见解析不计).
),且B,C,E三点在同一条直线上.请根据以上条件求出树DE的高度(测倾器的高度忽见解析不计).
在某市开展的“读中华经典,做书香少年”读书月活动中,围绕学生日人均阅读时间这一问题,对初二学生进行随机抽样调查.如图是根据调查结果绘制成的统计图(不完整),请你根据图中提供的信息解答下列问题:
(1)本次抽样调查的样本容量是多少?
(2)请将条形统计图补充完整.
(3)在扇形统计图中,计算出日人均阅读时间在1~1.5小时对应的圆心角度数.
(4)根据本次抽样调查,试估计该市12000名初二学生中日人均阅读时间在0.5~1.5小时的多少人.
如图,已知△ABC是等腰三角形,顶角∠BAC=α(α<60°),D是BC边上的一点,连接AD,线段AD绕点A顺时针旋转α到AE,过点E作BC的平行线,交AB于点F,连接DE,BE,DF.
(1)求证:BE=CD;
(2)若AD⊥BC,试判断四边形BDFE的形状,并给出证明.
有一个不透明口袋,装有分别标有数字1,2,3,4的4个小球(小球除数字不同外,其余
都相同),另有3张背面完全一样、正面分别写有数字1,2,3的卡片.小敏从口袋中任意摸出一个小球,小
颖从这3张背面朝上的卡片中任意摸出一张,然后计算摸出的小球和卡片上的两个数的积.
(1)请你用列表或画树状图的方法,求摸出的这两个数的积为6的概率;
(2)小敏和小颖做游戏,她们约定:若这两个数的积为奇数,小敏赢;否则,小颖赢.你认为该游戏公平吗?为什么?如果不公平,请你修改游戏规则,使游戏公平.
如图,一次函数y=ax+b的图象与反比例函数 的图象相交于A,B两点,与y轴交于点C,与x轴交于点D,点D的坐标为(-2,0),点A的横坐标是2,tan∠CDO=
的图象相交于A,B两点,与y轴交于点C,与x轴交于点D,点D的坐标为(-2,0),点A的横坐标是2,tan∠CDO= .
.
(1)求点A的坐标;
(2)求一次函数和反比例函数的解析式;
(3)求△AOB的面积.
为奖励在演讲比赛中获奖的同学,班主任派学习委员小明为获奖同学买奖品,要求每人一件.小明到文具店看了商品后,决定奖品在钢笔和笔记本中选择.如果买4个笔记本和2支钢笔,则需86元;如果买3个笔记本和1支钢笔,则需57元.
(1)求购买每个笔记本和钢笔分别为多少元;
(2)售货员提示,买钢笔有优惠,具体方法是:如果买钢笔超过10支,那么超出部分可以享受8折优惠,若买x(x>10)支钢笔需要花y元,请你求出y与x的函数关系式;
(3)在(2)的条件下,小明决定买同一种奖品,数量超过10个,请帮小明判断买哪种奖品省钱.
如图,AB为半圆的直径,O为圆心,C为圆弧上一点,AD垂直于过C点的切线,垂足为D,AB的延长线交直线CD于点E.
(1)求证:AC平分∠DAB;
(2)若AB=4,B为OE的中点,CF⊥AB,垂足为点F,求CF的长;
(3)如图2,连接OD交AC于点G,若 =
= ,求sin∠E的值.
,求sin∠E的值.
如图,在平面直角坐标系中,抛物线y=﹣ x2+bx+c与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
x2+bx+c与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
(1)求该抛物线的解析式;
(2)当点P在直线BC上方时,请用含m的代数式表示PG的长度;
(3)在(2)的条件下,是否存在这样的点P,使得以P、B、G为顶点的三角形与△DEH相似?若存在,求出此时m的值;若不存在,请说明理由.


 并把解集在数轴上表示出来.
并把解集在数轴上表示出来.
 ,其中x满足
,其中x满足
 粤公网安备 44130202000953号
粤公网安备 44130202000953号