有一个不透明口袋,装有分别标有数字1,2,3,4的4个小球(小球除数字不同外,其余
都相同),另有3张背面完全一样、正面分别写有数字1,2,3的卡片.小敏从口袋中任意摸出一个小球,小
颖从这3张背面朝上的卡片中任意摸出一张,然后计算摸出的小球和卡片上的两个数的积.
(1)请你用列表或画树状图的方法,求摸出的这两个数的积为6的概率;
(2)小敏和小颖做游戏,她们约定:若这两个数的积为奇数,小敏赢;否则,小颖赢.你认为该游戏公平吗?为什么?如果不公平,请你修改游戏规则,使游戏公平.
相关知识点
推荐套卷
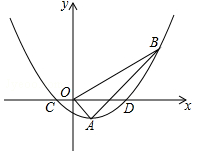
 .
.
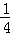 x2上任意一点到点(0,1)的距离与到直线y=﹣1的距离相等,你可以利用这一性质解决问题.
x2上任意一点到点(0,1)的距离与到直线y=﹣1的距离相等,你可以利用这一性质解决问题.
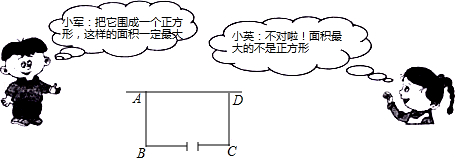
 ,1)、B(2,0)、O(0,0),反比例函数y=
,1)、B(2,0)、O(0,0),反比例函数y=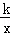 图象经过点A.
图象经过点A.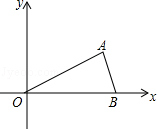
 粤公网安备 44130202000953号
粤公网安备 44130202000953号