某校在基地参加社会实践话动中，带队老师考问学生：基地计划新建一个矩形的生物园地，一边靠旧墙（墙足够长），另外三边用总长69米的不锈钢栅栏围成，与墙平行的一边留一个宽为3米的出入口，如图所示，如何设计才能使园地的而积最大？下面是两位学生争议的情境：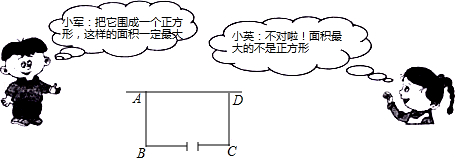
请根据上面的信息，解决问题：
（1）设AB=x米（x＞0），试用含x的代数式表示BC的长；
（2）请你判断谁的说法正确，为什么？
相关试题
2014年某敬老院老人年龄数据如下（单位：岁）：
85、64、78、56、91、71、59、75、98、83、77、79、81、94、86、68．
（1）请你完成下面的统计表．
| 年龄（岁） |
90～100 |
80～89 |
70～79 |
60～69 |
60以下 |
| 人数 |
（2）在这个敬老院中，年龄最大的老人是 岁．
（3）80岁以上的老人占敬老院老人总数的 ．
，去年生产了多少件？
，全校少先队员是全校人数的80%，少先队员有多少人？
千米，第二周修了
千米，第三周修的比前两周的总和少
千米．
粤公网安备 44130202000953号