安徽省安庆市初中毕业班正月联考数学试卷
如图,在下列网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正弦值是( )
A. B.
B. C.
C. D.
D.
如图,⊙O的直径CD垂直弦AB于点E,且CE=2,DE=8,则AB的长为( )
| A.2 | B.4 | C.6 | D.8 |
下列四个函数中,一定是二次函数的是( )
A.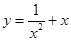 |
B.y=ax2+bx+c |
| C.y=x2﹣(x+7)2 | D.y=(x+1)(2x﹣1) |
如图是一个旋转对称图形,要使它旋转后与自身重合,至少应将它绕中心逆时针方向旋转的度数为( )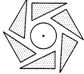
| A.30° | B.60° | C.120° | D.180° |
拦水坝横断面如图所示,迎水坡AB的坡比是1: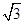 ,坝高BC=10m,则坡面AB的长度是( )
,坝高BC=10m,则坡面AB的长度是( )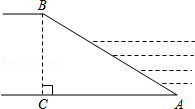
| A.15m | B.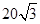 m m |
C.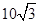 m m |
D.20m |
如图,在△ABC中,点D在边AB上,BD=2AD,DE∥BC交AC于点E,若线段DE=5,则线段BC的长为( )
| A.7.5 | B.10 | C.15 | D.20 |
如图,在平面直角坐标系中,点A是x轴正半轴上的一个定点,点P是双曲线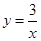 (x>0)上的一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会( )
(x>0)上的一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会( )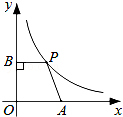
| A.逐渐增大 | B.不变 | C.逐渐减小 | D.先增大后减小 |
二次函数y=ax2+bx+c(a≠0)的图象如图,关于该二次函数,下列说法错误的是( )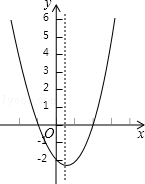
| A.函数有最小值 |
B.对称轴是直线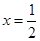 |
C.当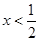 时,y随x的增大而减小 时,y随x的增大而减小 |
| D.当﹣1<x<2时,y>0 |
如图,对称轴平行于y轴的抛物线与x轴交于(1,0),(3,0)两点,則它的对称轴为_________ .
如图,双曲线 经过Rt△BOC斜边上的点A,且满足
经过Rt△BOC斜边上的点A,且满足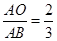 ,与BC交于点D,S△BOD=21,求k= _________ .
,与BC交于点D,S△BOD=21,求k= _________ .
如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=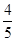 .下列结论:
.下列结论: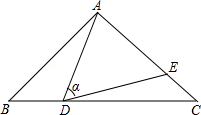
①△ADE∽△ACD;
②当BD=6时,△ABD与△DCE全等;
③△DCE为直角三角形时,BD为8或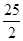 ;
;
④0<CE≤6.4.
其中正确的结论是_________ .(把你认为正确结论的序号都填上)
已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).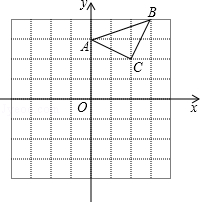
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是_________ ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是_________ ;
(3)△A2B2C2的面积是_________ 平方单位.
如图,在平行四边形ABCD中,点G是BC延长线上一点,AG与BD交于点E,与DC交于点F,如果AB=m,CG=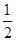 BC,
BC,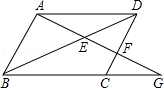
求:(1)DF的长度;
(2)三角形ABE与三角形FDE的面积之比.
如图,用一根6米长的笔直钢管弯折成如图所示的路灯杆ABC,AB垂直于地面,线段AB与线段BC所成的角∠ABC=120°,若路灯杆顶端C到地面的距离CD=5.5米,求AB长.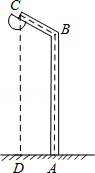
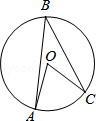
如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.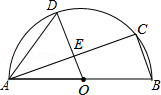
(1)若∠B=70°,求∠CAD的度数;
(2)若AB=4,AC=3,求DE的长.
如图的⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,并与AB延长线交于点E.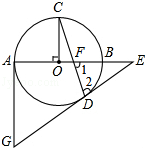
(1)求证:∠1=∠2.
(2)已知:OF:OB=1:3,⊙O的半径为3,求AG的长.
如图,已知二次函数y=ax2+bx+c的图象过A(2,0),B(0,﹣1)和C(4,5)三点.
(1)求二次函数的解析式;
(2)设二次函数的图象与x轴的另一个交点为D,求点D的坐标;
(3)在同一坐标系中画出直线y=x+1,并写出当x在什么范围内时,一次函数的值大于二次函数的值.
如图所示的晾衣架,支架主视图的基本图形是菱形,其示意图如图2,晾衣架伸缩时,点G在射线DP上滑动,∠CED的大小也随之发生变化,已知每个菱形边长均等于20cm,且AH=DE=EG=20cm.
(1)当∠CED=60°时,求C、D两点间的距离;
(2)当∠CED由60°变为120°时,点A向左移动了多少cm?(结果精确到0.1cm)
(3)设DG=xcm,当∠CED的变化范围为60°~120°(包括端点值)时,求x的取值范围.(结果精确到0.1cm)(参考数据 ≈1.732)
≈1.732)
如图,在平行四边形ABCD中,对角线AC、BD交于点O,M为AD中点,连接CM交BD于点N,且ON=1。
(1)求BD的长
(2)若△DCN的面积为2,求四边形ABNM的面积。
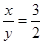 ,那么下列等式中,不一定正确的是( )
,那么下列等式中,不一定正确的是( )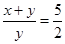
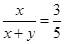
 (k≠0)在同一坐标系中的图象大致是( )
(k≠0)在同一坐标系中的图象大致是( )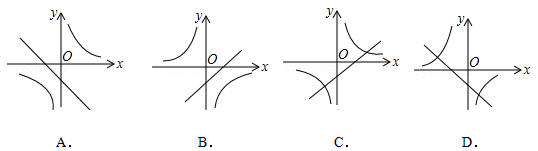
 粤公网安备 44130202000953号
粤公网安备 44130202000953号