初中数学一次函数的最值解答题

甲、乙两名运动员进行长跑训练，两人距终点的路程（米）与跑步时间之间的函数关系如图所示，根据图象所提供的信息解答问题：

（1）他们在进行       米的长跑训练，在0<<15的时间内，速度较快的人是       （填“甲”或“乙”）；
（2）求乙距终点的路程（米）与跑步时间之间的函数关系式；
（3）当=15时，两人相距多少米？
（4）在15<<20的时间段内，求两人速度之差．

一汽车租赁公司拥有某种型号的汽车100辆．公司在经营中发现每辆车的月租金x（元）与每月租出的车辆数（y）有如下关系：

（1）观察表格，用所学过的一次函数、反比例函数或二次函数的有关知识求出每月租出的车辆数y（辆）与每辆车的月租金x（元）之间的关系式．
（2）已知租出的车每辆每月需要维护费150元，未租出的车每辆每月需要维护费50元．每辆车的月租金定为多少元时，才能使公司获得最大月收益？请求出公司的最大月收益是多少元．

（本小题满分10分）小刚和小强相约晨练跑步，小刚比小强早1分钟离开家门，3分钟后迎面遇到从家跑来的小强．两人同路并行跑了2分钟后，决定进行长跑比赛，比赛时小刚的速度始终是180米/分，小强的速度始终是220米/分．下图是两人之间的距离y（米）与小刚离开家的时间x（分钟）之间的函数图象，根据图象回答下列问题：

（1）两人相遇之前，小刚的速度是     米/分，小强的速度是     米/分；
（2）求两人比赛过程中y与x之间的函数关系式；

黄岩岛是我国南沙群岛的一个小岛，渔产丰富．一天某渔船离开港口前往该海域捕鱼．捕捞一段时间后，发现一外国舰艇进入我国水域向黄岩岛驶来，渔船向渔政部门报告，并立即返航．渔政船接到报告后，立即从该港口出发赶往黄岩岛．下图是渔政船及渔船与港口的距离S和渔船离开港口的时间t之间的函数图象．（假设渔船与渔政船沿同一航线航行）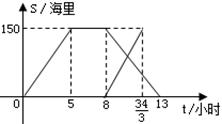

（1）直接写出渔船离港口的距离S和它离开港口的 时间t的函数关系式．
（2）求渔船和渔政船相遇时，两船与黄岩岛的距离．
（3）在渔政船驶往黄岩岛的过程中，求渔船从港口出发经过多长时间与渔政船相距30海里？

小李从福安通过某快递公司给在上海的外婆寄一盒穆阳水蜜桃，快递时，他了解到这个公司除了收取每次6元包装费外，水蜜桃不超过1kg收费22元，超过1kg，则超出部分每千克收费10元，设该公司从福安到上海快寄水蜜桃的费用为y（元），所寄水蜜桃为x（kg）
（1）求y与x之间的函数关系式；
（2）已知小李给外婆快寄了2．5kg水蜜桃，请你求出这次快寄的费用是多少元？

南海地质勘探队在南沙群岛的一个小岛发现很有价值的A、B两种矿石，A矿石大约565吨，B矿石大约500吨，上报公司，要一次性将两种矿石运往冶炼厂，需要不同型号的甲、乙两种货船共30艘，甲货船每艘运费1000元，乙货船每艘费用1200元。
（1）设运送这些矿石的总运费为y元，若使用甲货船x艘，请写出y与x之间的函数关系式；
（2）如果甲货船最多可装A矿石20吨和B矿石15吨，乙货船最多可装A矿石15吨和B矿石25吨，装矿石时按此要求安排甲、乙两种货船，共有几中安排方案？哪种方案运费最低并求出最低费用。

某游泳馆普通票价20元/张，暑假为了促销，新推出两种优惠卡：
① 金卡售价600元/张，每次凭卡不再收费；
② 银卡售价150元/张，每次凭卡另收10元.
暑期普通票正常出售，两种优惠卡仅限暑期使用，不限次数. 设游泳x次时，所需总费用为y元.
（1）分别写出选择银卡、普通票消费时，y与x之间的函数关系式；
（2）在同一个坐标系中，若三种消费方式对应的函数图像如图所示，请求出点A、B、C的坐标；
（3）请根据函数图象，直接写出选择哪种消费方式更合算.

阅读下面材料：小明研究了这样一个问题：求使得等式成立的x的个数．小明发现，先将该等式转化为，再通过研究函数的图象与函数的图象（如图）的交点，使问题得到解决．

（1）当k＝1时，使得原等式成立的x的个数为_______；
（2）当0＜k＜1时，使得原等式成立的x的个数为_______；
（3）当k＞1时，使得原等式成立的x的个数为_______．
参考小明思考问题的方法，解决问题：关于x的不等式只有一个整数解，求的取值范围．

如图，矩形OABC中， A（0，5），C（4，0），正比例函数的图象经过点B．

（1）求正比例函数的表达式；
（2）反比例函数的图象与正比例函数的图象和边BC围成的阴影区域BNM如图所示,请直接写出阴影区域中横纵坐标都是整数的点的坐标（不包括边界）．

秋交会前夕，我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销．经过调查，得到如下数据：

（1）把上表中x、y的各组对应值作为点的坐标，在下面的平面直角坐标系中描出相应的点，猜想y与x的函数关系，并求出函数关系式；
（2）当销售单价定为多少时，工艺厂试销该工艺品每天获得的利润为8000元？（利润＝销售总价－成本总价）
（3）市物价部门规定，该工艺品销售单价最高不能超过35元/件，那么销售单价定为多少时，工艺厂试销该工艺品每天获得的利润最大？

某商店销售10台A型和20台B型电脑的利润为4000元，销售20台A型和10台B型电脑的利润为3500元．
（1）求每台A型电脑和B型电脑的销售利润；
（2）该商店计划一次购进两种型号的电脑共100台，其中B型电脑的进货量不超过A型电脑的2倍，设购进A型电脑x台，这100台电脑的销售总利润为y元．
①求y关于x的函数关系式；
②该商店购进A型、B型电脑各多少台，才能使销售总利润最大？
（3）实际进货时，厂家对A型电脑出厂价下调m（0＜m＜100）元，且限定商店最多购进A型电脑70台，若商店保持同种电脑的售价不变，请你根据以上信息及（2）中条件，设计出使这100台电脑销售总利润最大的进货方案．

如图，在直角坐标系中，A（0，4）、C（3，0）．

（1）①画出线段AC关于y轴对称线段AB；
②将线段CA绕点C顺时针旋转一个角，得到对应线段CD，使得AD∥x轴，请画出线段CD．
（2）若直线平分（1）中四边形ABCD的面积，请直接写出实数k的值．

（本题12分）已知直线AB分别交、轴于A（4，0）、B两点，C（－4，）为直线AB上且在第二象限内一点，若△COA的面积为8，

（1）如图1，求C点坐标；
（2）如图2，点M为第二象限内一点，CM⊥OM于M，CN⊥轴于N，连MN，求证：的值；
（3）如图3，过C作CN⊥轴于N，G为第一象限内一点，且∠NGO＝45°，试探究GC²、GN²与GO²之间的数量关系并说明理由.

（10 分）我市某风景区门票价格如图所示黄冈赤壁旅游公司有甲、乙两个旅行团队，计划在“五一”小黄金周期间到该景点游玩，两团队游客人数之和为120 人，乙团队人数不超过50 人．设甲团队人数为x 人，如果甲、乙两团队分别购买门票，两团队门票款之和为W 元．
  
（1）求W 关于x 的函数关系式，并写出自变量x 的取值范围；
（2）若甲团队人数不超过100 人，请说明甲、乙两团队联合购票比分别购票最多可节约多少钱；
（3）“五一”小黄金周之后，该风景区对门票价格作了如下调整：人数不超过50 人时，门票价格不变；人数超过50 人但不超过100 人时，每张门票降价a 元；人数超过100 人时，每张门票降价2a 元．在（2）的条件下，若甲、乙两个旅行团队“五一”小黄金周之后去游玩，最多可节约3400 元，求a 的值．

水平放置的容器内原有210毫米高的水，如图．将若干个球逐一放入容器中，每放入一个大球水面就上升4毫米，每放入一个小球水面就上升3毫米，假定放入容器中的所有球完全浸没水中且水不溢出，设水面高为y毫米．

（1）只放入大球，且个数为x_大，求y与x_大的函数关系式（不必写出x_大的范围）；
（2）仅放入6个大球后，开始放入小球，且小球个数为x_小．
①求y与x_小的函数关系式（不必写出x_小的范围）；
②限定水面高不超过260毫米，最多放入几个小球？