某人购进一批苹果到集贸市场零售,已知卖出的苹果数量x(千克)与售价y(元)之间的关系如下表:
| 数量x/千克 |
1 |
2 |
3 |
4 |
| 售价y/元 |
1.2+0.1 |
2.4+0.1 |
3.6+0.1 |
4.8+0.1 |
(1)写出y与x的关系式
(2)卖多少千克的苹果,可得14.5元?若卖出苹果10千克,则应得多少元?
如图,直线y=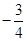 x+6与x轴交于点B,与y 轴交于点A.以AB为边画正方形ABCD.
x+6与x轴交于点B,与y 轴交于点A.以AB为边画正方形ABCD.
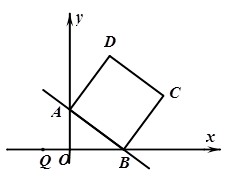
(1)求△AOB的面积;
(2)求点C的坐标;
(3)已知点Q(-4,0),点P从点Q出发,以每秒2个单位的速度沿x轴的正方向运动,设运动时间为t秒,当t为何值时,△PBC是等腰三角形.
甲、乙两辆汽车分别从A、B两地同时出发,沿同一条公路相向而行,乙车出发2h后休息,与甲车相遇后,继续行驶.设甲、乙两车与B地的路程分别为y甲(km),y乙(km),甲车行驶的时间为x(h),y甲、y乙与x之间的函数图像如图所示,结合图像解答下列问题: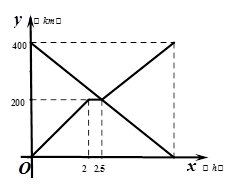
(1)A、B两地相距 km;
(2)求乙车与甲车相遇后,y乙与x之间的函数表达式;
(3)甲、乙两辆汽车出发多长时间两车相距50km.
已知 与
与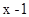 成正比例,当
成正比例,当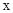 =-1时,
=-1时,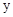 =4,
=4,
(1)求出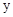 与
与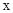 的函数表达式;
的函数表达式;
(2)设点(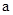 ,-2)在这个函数的图像上,求
,-2)在这个函数的图像上,求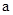 的值.
的值.
写出同时具备下列两个条件的一次函数表达式(写出一个即可) .
(1)y随着x的增大而减小;
(2)图像经过点(0,-3)
(本小题6分)如图,直线AB与y轴交于点A,与x轴交于点B,点A的纵坐标、点B的横坐标如图所示.

(1)求直线AB的解析式;
|
(2)点P在直线AB上,是否存在点P使得△AOP的面积为1,如果有请直接写出所有满足条件的点P的坐标
(本小题6分))已知一次函数y=kx+b的图象经过点(-1, -5),且与正比例函数y= x的图象相交于点(2,a),求:
(1)a的值
(2)k,b的值
(3)这两个函数图象与y轴所围成的三角形的面积。
画出函数y=- x+3的图象,根据图象回答下列问题:
x+3的图象,根据图象回答下列问题:
(1)求方程- x+3=0的解;
x+3=0的解;
(2)求不等式- x+3<0的解集;
x+3<0的解集;
(3)当x取何值时,y≥0.
一台拖拉机工作时,每小时耗油6L,已知油箱中有油40L.
(1)设拖拉机的工作时间为t小时,油箱中的剩余油量为Q升,求出Q(升)与t(小时)之间的函数关系式;
(2)求出自变量的取值范围;
(3)当油箱内剩余油10L时,这台拖拉机已工作了几小时?
如图是甲、乙两人同一地点出发后,路程随时间变化的图象.
(1)此变化过程中,__________是自变量,_________是因变量.
(2)甲的速度是 ________千米/时,乙的速度是________千米/时
(3)6时表示_________________________
(4)路程为150千米,甲行驶了____小时,乙行驶了_____小时.
(5)9时甲在乙的________(前面、后面、相同位置)
(6)分别写出甲乙两人行驶的路程s(千米)与行驶的时间t(小时)的函数关系式(不要求写出自变量的取值范围)
S甲=___________________________
S乙=___________________________
(本题8分)小敏上午8:00从家里出发,骑车去一家超市购物,然后从这家超市返回家中。小敏离家的路程 (米)和所经过的时间
(米)和所经过的时间 之间的函数图象如图所示。请根据图象回答下列问题:
之间的函数图象如图所示。请根据图象回答下列问题:
(1)小敏去超市途中的速度是多少?在超市逗留了多少时间?
(2)小敏几点几分返回到家?
高铁的开通,给衢州市民出行带来了极大的方便,“五一”期间,乐乐和颖颖相约到杭州市的某游乐园游玩,乐乐乘私家车从衢州出发1小时后,颖颖乘坐高铁从衢州出发,先到杭州火车站,然后再转车出租车取游乐园(换车时间忽略不计),两人恰好同时到达游乐园,他们离开衢州的距离y(千米)与乘车时间t(小时)的关系如图所示.
请结合图象解决下面问题: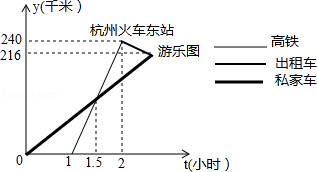
(1)高铁的平均速度是每小时多少千米?
(2)当颖颖达到杭州火车东站时,乐乐距离游乐园还有多少千米?
(3)若乐乐要提前18分钟到达游乐园,问私家车的速度必须达到多少千米/小时?
如图,直线y=2x与反比例函数 (k≠0,x>0)的图像交于点A(1,a),点B是此反比例函数图形上任意一点(不与点A重合),BC⊥x轴于点C.
(k≠0,x>0)的图像交于点A(1,a),点B是此反比例函数图形上任意一点(不与点A重合),BC⊥x轴于点C.
(1)求k的值.
(2)求△OBC的面积.
胡老师计划组织朋友暑假去革命圣地延安两日游,经了解,现有甲、乙两家旅行社比较合适,报价均为每人640元,且提供的服务完全相同,针对组团两日游的游客,甲旅行社表示,每人都按八五折收费;乙旅行社表示,若人数不超过20人,每人都按九折收费,超过20人,则超出部分每人按七五折收费。假设组团参加甲、乙两家旅行社两日游的人数均为x人。
(1)请分别写出甲、乙两家旅行社收取组团两日游的总费用y(元)与x(人)之间的函数
关系式;
(2)若胡老师组团参加两日游的人数共有32人,请你通过计算,在甲、乙两家旅行社中,
帮助胡老师选择收取总费用较少的一家。
某苹果生产基地,用30名工人进行采摘或加工苹果,每名工人只能做其中一项工作。苹果的销售方式有两种:一种是可以直接出售;另一种是可以将采摘的苹果加工成罐头出售。直接出售每吨获利4000元;加工成罐头出售每吨获利10000元。采摘的工人每人可以采摘苹果0.4吨 ;加工罐头的工人每人可加工0.3吨。设有x名工人进行苹果采摘,全部售出后 ,总利润为y元 .
(1)求y与x的函数关系式。
(2)如何分配工人才能活力最大