初中数学一次函数的最值解答题

现有甲、乙两个容器，分别装有进水管和出水管，两容器的进出水速度不变，先打开乙容器的进水管，2分钟时再打开甲容器的进水管，又过2分钟关闭甲容器的进水管，再过4分钟同时打开甲容器的进、出水管．直到12分钟时，同时关闭两容器的进出水管，打开和关闭水管的时间忽略不计。容器中的水量y（升）与乙容器注水时间x之间的关系如图所示:

（1）求甲容器的进、出水速度．
（2）甲容器进、出水管都关闭后，是否存在两容器的水量相等。若存在，求出此时的时间．
（3）若使两容器第12分钟时水量相等，则乙容器6分钟后进水速度应变为多少？

如图，已知在平面直角坐标系xoy中，O是坐标原点，点A（2，5）在反比例函数y=的图象上，过点A的直线y=x+b交x轴于点B．

（1）求k和b的值；
（2）求△OAB的面积．

在一条笔直的公路旁依次有A、B、C三个村庄，甲、乙两人同时分别从A、B两村出发，甲骑摩托车，乙骑电动车沿公路匀速驶向C村，最终到达C村．甲、乙两人到C村的距离y₁，y₂（km）与行驶时间x（h）之间的函数关系如图所示，请回答下列问题：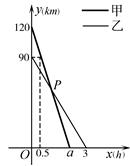

（1）A、C两村间的距离为   km；
（2）求a的值和点P的坐标，并解释该点坐标所表示的实际意义；
（3）乙在行驶过程中，何时距甲10km？

甲、乙两商场各自推出不同的优惠方案：在甲商场累计购物超过100元后，超出100元的部分按90%收费；在乙商场累计购物超过50元后，超出50元的部分按95%收费，设小红在同一商场累计购物x元，其中x＞100．
（1）根据题意，填写下表（单位：元）：

（2）当x取何值时，小红在甲、乙两商场的实际花费金额相同？
（3）请你根据小红累计购物的金额选择花费较少的商场？

喝绿茶前需要烧水和泡茶两个工序，即需要将电热壶中的水烧到100℃，然后停止烧水，等水温降低到适合的温度时再泡茶，烧水时水温 （℃）与时间菇（min）成一次函数关系；停止加热1分钟后（1分钟内水温不变），水壶中水的温度y（℃）与时间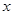 （min）近似于反比例函数关系（如图）．已知水壶中水的初始温度是20℃，降温过程中水温不低于20℃．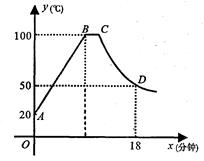

（1）求出图中AB所在直线对应的函数关系式，并且写出自变量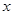的取值范围；
（2）从水壶中的水烧开（100℃）降到80℃就可以进行泡制绿茶，问从水烧开到泡茶需要等待多长时间?

在平面直角坐标系中，一次函数的图象与x轴、y轴相交于点A（，0），B（0，）两点，二次函数的图象经过点A．

（1）求一次函数的表达式；
（2）若二次函数的图象的顶点在直线AB上，求m，n；
（3）①设时，当时，求二次函数的最小值；
②反之若时，二次函数的最小值为，求m，n的值．

甲、乙两车分别从A、B两地同时出发相向而行，并以各自的速度匀速行驶，甲车与乙车相遇后休息半小时，再按原速度继续前进到达B地；乙车从B地直接到达A地；两车到达各自目的地后即停止．如图是甲、乙两车和B地的距离y（千米）与甲车出发时间x（小时）的函数图象．

（1）甲车的速度是       ，m=     ；
（2）请分别写出两车在相遇前到B地的距离y（千米）与甲车出发时间x（小时）的函数关系式；
（3）当乙车行驶多少时间时，甲乙两车的距离是280千米．

2015“两相和”杯群星演唱会在我市体育馆进行，市文化局、广电局
在策划本次活动，在与单位协商团购票时推出两种方案．设购买门票数为x（张），总费
用为y（元）．
方案一：若单位赞助广告费8000元，则该单位所购门票的价格为每张50元；（总费用
＝广告赞助费+门票费）
方案二：直接购买门票方式如图所示．

解答下列问题：
（1）方案一中，y与x的函数关系式为              ；
方案二中，当0≤x≤100时，y与x的函数关系式为           ，
当x＞100时，y与x的函数关系式为             ；
（2）甲、乙两单位分别采用方案一、方案二购买本场演唱会门票共700张，花去总费用计56000元，求甲、乙两单位各购买门票多少张？

某工厂在生产过程中每消耗1万度电可以产生产值5.5万元．电力公司规定，该工厂每月用电量不得超过16万度；月用电量不超过4万度时，单价都是1万元/万度；超过4万度时，超过部分电量单价将按用电量进行调整，电价y与月用电量x的函数关系可以用如图来表示．（效益＝产值－用电量×电价）；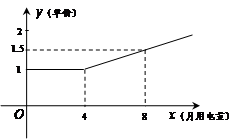

（1）设工厂的月效益为z（万元），写出z与月用电量x（万度）之间的函数关系式，并写出自变量的取值范围；
（2）求工厂最大月效益．

“六一”期间，小张购进100只两种型号的文具进行销售，其进价和售价之间的关系如下表：

（1）小张如何进货，使进货款恰好为1300元？
（2）要使销售文具所获利润最大，且所获利润不超过进货价格的40%，请你帮小张设计一个进货方案，并求出其所获利润的最大值．

小明到服装店参加社会实践活动，服装店经理让小明帮助解决以下问题：
服装店准备购进甲乙两种服装，甲种每件进价80元，售价120元；乙种每件进价60元，售价90元．计划购进两种服装共100件，其中甲种服装不少于65件。
（1）若购进这100件服装的费用不得超过7500，则甲种服装最多购进多少件？
（2）在（1）的条件下，该服装店对甲种服装以每件优惠a（0＜a＜20）元的价格进行优惠促销活动，乙种服装价格不变，那么该服装店应如何调整进货方案才能获得最大利润？

某商店以40元/千克的单价新进一批茶叶，经调查发现，在一段时间内，销售量y（千克）与销售单价x（元/千克）之间的函数关系如图所示．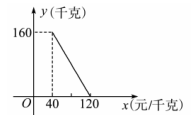

（1）根据图象，求y与x的函数关系式；
（2）商店想在销售成本不超过3000元的情况下，使销售利润达到2400元，销售单价应定为多少？

甲、乙两车从A地驶向B地，并以各自的速度匀速行驶，甲车比乙车早行驶2h，并且甲车途中休息了0．5h，如图是甲乙两车行驶的距离y（km）与时间x（h）的函数图象．

（1）求出图中m，a的值；
（2）求出甲车行驶路程y（km）与时间x（h）的函数解析式，并写出相应的x的取值范围；
（3）当乙车行驶多长时间时，两车恰好相距50km．

广安某水果点计划购进甲、乙两种新出产的水果共140千克，这两种水果的进价、售价如表所示：

	进价（元/千克）	售价（元/千克）
甲种	5	8
	9	13

（1）若该水果店预计进货款为1000元，则这两种水果各购进多少千克？
（2）若该水果店决定乙种水果的进货量不超过甲种水果的进货量的3倍，应怎样安排进货才能使水果点在销售完这批水果时获利最多？此时利润为多少元？

（本题10分）已知一次函数的图像经过点，，且与正比例函数的图像相交于点，．
（1）求的值；
（2）求一次函数的解析式；
（3）求这两个函数图像与轴所围成的三角形面积．（画图解答）