浙江省台州市黄岩区中考第一次模拟考试数学试卷

－2的相反数是 （ ）

A．2

B．－2

C．

D．－

用4个完全相同的小正方体组成如左下图所示的立体图形，那么它的主视图是（ ）
  

小星同学参加体育测试的五次立定跳远的成绩（单位：米）是：1． 2，1．3，1．2，1．0，1．1．这组数据的众数是 （ ）

中国航母辽宁舰是中国人民海军第一艘可以搭载固定翼飞机的航空母舰，满载排水量为67500吨，这个数据用科学记数法表示为         （ ）

掷一枚质地均匀的硬币10次，则下列说法正确的是 （ ）

如图，在地面上的点A处测得树顶B的仰角α=75º， 若AC＝6米，则树高BC为 （ ）

A．6sin75º米

B．米

C．米

D．6tan75º米

某药品经过两次降价，每瓶零售价由100元降为81元．已知两次降价的百分率都为x，那么x满足的方程是 （ ）

A．100=81	B．100=81
C．100（1－2x）=81	D．100=81

已知一等腰三角形的腰长为5，底边长为4，底角为α．满足下列条件的三角形与已知三角形不一定全等的是（   ）

学习了一次函数、二次函数、反比例函数后，爱钻研的小敏尝试用同样的方法研究函数y=，从而得出以下命题：
（1）当x＞0时，y的值随着x的增大而减小；
（2）y的值有可能等于3；
（3）当x＞0时，y的值随着x的增大越来越接近3；
（4）当y＞0时，x＞0或x＜－．
你认为真命题是 （ ）

如图，边长为2的正方形ABCD的顶点A、B在一个半径为2的圆上， 顶点C、D在圆内，将正方形ABCD沿圆的内壁作无滑动的滚动．当滚动一周回到原位置时，点C运动的路径长为 （ ）

A．2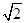x          B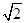．（+1）π          C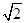．（+2）π          D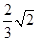．（+1）π 

分解因式：a²﹣9=         ．

在函数y=中，自变量x的取值范围是        ．

如图，l∥m，矩形ABCD的顶点B在直线m上，则∠α=          度．

在一个口袋中有4个完全相同的小球，把它们分别标号为1，2，3，4，随机地摸取一个小球然后放回，再随机地摸出一个小球，则两次取出的小球的标号相同的概率是         ．

已知函数y=k－2x－k－2的图象与坐标轴有两个交点，则k的值为         ．

如图，点O为弧AB所在圆的圆心，OA⊥OB，点P在弧AB上，AP的延长线与OB的延长线交于点C，过点C作CD⊥OP于D．若OP=3，PD=1，则OC=          ．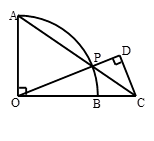

（1）计算：2sin45°－； 
（2）化简：（x－1）（x+2）+．

图①、图②均为7×6的正方形网格，点A、B、C在格点上．

（1）在图①中确定格点D，并画出以A、B、C、D为顶点的四边形， 使其为轴对称图形．（画一个即可）
（2）在图②中确定格点E，并画出以A、B、C、E为顶点的四边形，使其为中心对称图形．（画一个即可）

我区积极开展“体育大课间”活动，引导学生坚持体育锻炼．某校根据实际情况，决定主要开设A：乒乓球，B：篮球，C：跑步，D：足球四种运动项目．为了解学生最喜欢哪一种项目，随机抽取了部分学生进行调查，并将调查结果绘制成如下统计图．请你结合图中信息解答下列问题：

（1）求样本中最喜欢B项目的人数百分比和其所在扇形图中的圆心角的度数；
（2）请把条形统计图补充完整；
（3）已知该校有1000人，请根据样本估计全校最喜欢足球的人数是多少？

如图，已知在平面直角坐标系xoy中，O是坐标原点，点A（2，5）在反比例函数y=的图象上，过点A的直线y=x+b交x轴于点B．

（1）求k和b的值；
（2）求△OAB的面积．

如图，已知AB是⊙O的直径，直线CD与⊙O相切于点C，AC平分∠DAB．

（1）求证：AD⊥CD；
（2）若AD=2，AC=，求AB的长．

某工厂生产的某种产品按质量分为10个等级．第1级（最低级）产品每天能生产95件，每件利润6元．已知每提高一个级别，每件利润增加2元，但每天产量减少5件．
（1）若生产第3级产品，则每天产量为 件，每件利润为 元；
（2）若生产第x级产品一天的总利润为y元（其中x为正整数，且1≤x≤10），求出y关于x的函数解析式；
（3）若生产第x级的产品一天的总利润为1120元，求该产品的质量等级．

如图，已知抛物线y=与x轴交于A、B两点．

（1）点A的坐标是      ，点B的坐标是      ，抛物线的对称轴是直线         ；
（2）将抛物线向上平移m个单位，与x轴交于C、D两点（点C 在点D的左边）．若CD：AB=3：4，求m的值；
（3）点P是（2）中平移后的抛物线上y轴右侧部分的点，直线y=2x+b（b0）与 x、y轴分别交于点E、F．若以EF为直角边的三角形PEF与△OEF相似，直接写出点P的坐标．

定义：两组邻边分别相等的四边形叫做筝形．
（1）请写出除定义外的性质和判定猜想各一条，并从定义出发证明你的判定猜想．
（2）筝型ABCD中，对角线AC，BD相交于点O．
①如图1，若BD=CO，求tan∠BCD的值．
②如图2，若∠DAC=∠BCD=72º，求AD:CD的值．
（3）如图3，把△ABD沿着对角线BD翻折，A点落在对角线AC上的E点．如果△AOD中，一个内角是另一个内角的2倍，且阴影部分图形的面积等于四边形ABED的面积，直接写出的值．