定义：两组邻边分别相等的四边形叫做筝形．
（1）请写出除定义外的性质和判定猜想各一条，并从定义出发证明你的判定猜想．
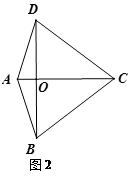
（2）筝型ABCD中，对角线AC，BD相交于点O．
①如图1，若BD=CO，求tan∠BCD的值．
②如图2，若∠DAC=∠BCD=72º，求AD:CD的值．
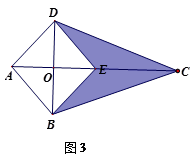
（3）如图3，把△ABD沿着对角线BD翻折，A点落在对角线AC上的E点．如果△AOD中，一个内角是另一个内角的2倍，且阴影部分图形的面积等于四边形ABED的面积，直接写出
的值．
相关试题
已知△ABC中，∠ABC=90゜，AB=BC，点A、B分别是x轴和y轴上的一动点．
（1）如图1，若点C的横坐标为4，求点B的坐标；
（2）如图2，BC交x轴于D，AD平分∠BAC，若点C的纵坐标为3，A（5，0），求点D的坐标．
（3）如图3，分别以OB、AB为直角边在第三、四象限作等腰直角△OBF和等腰直角△ABE，EF交y轴于M，求S△BEM：S△ABO．
相关知识点
推荐套卷
粤公网安备 44130202000953号