（本题10分）已知一次函数
的图像经过点
，
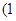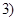，且与正比例函数
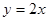的图像相交于点
，
．
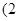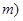（1）求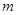
的值；
（2）求一次函数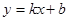
的解析式；
（3）求这两个函数图像与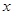
轴所围成的三角形面积．（画图解答）
相关知识点
推荐套卷
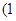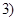（本题10分）已知一次函数的图像经过点，，且与正比例函数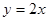的图像相交于点，．
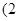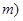（1）求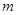的值；
（2）求一次函数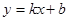的解析式；
（3）求这两个函数图像与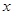轴所围成的三角形面积．（画图解答）
粤公网安备 44130202000953号