若二次函数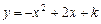 的部分图象如图所示,
的部分图象如图所示,
则关于x的一元二次方程 的一个解
的一个解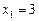 ,另一个解
,另一个解 ▲ ;
▲ ;
已知抛物线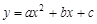 的开口向下,顶点坐标为(2,-3) ,那么该抛物线有( ▲ )
的开口向下,顶点坐标为(2,-3) ,那么该抛物线有( ▲ )
| A.最小值 -3 | B.最大值-3 | C.最小值2 | D.最大值2 |
△ABC中,∠A=∠B=30°,AB=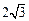 .把△ABC放在平面直角坐标系中,使AB的中点位于坐标原点O(如图),△ABC可以绕点O作任意角度的旋转.
.把△ABC放在平面直角坐标系中,使AB的中点位于坐标原点O(如图),△ABC可以绕点O作任意角度的旋转.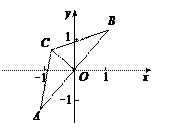
(1) 当点B在第一象限,纵坐标是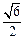 时,求点B的横坐标;
时,求点B的横坐标;
(2) 如果抛物线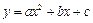 (a≠0)的对称轴经过点C,请你探究:
(a≠0)的对称轴经过点C,请你探究:
① 当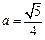 ,
,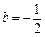 ,
,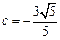 时,A,B两点是否都在这条抛物线上?并说明理由;
时,A,B两点是否都在这条抛物线上?并说明理由;
② 设b=-2am,是否存在这样的m的值,使A,B两点不可能同时在这条抛物线上?若存在,直接写出m的值;若不存在,请说明理由.
(本小题满分12分)
在平面直角坐标系xOy中,抛物线的解析式是y =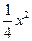 +1,点C的坐标为(–4,0),平行四边形OABC的顶点A,B在抛物线上,AB与y轴交于点M,已知点Q(x,y)在抛物线上,点P(t,0)在x轴上.
+1,点C的坐标为(–4,0),平行四边形OABC的顶点A,B在抛物线上,AB与y轴交于点M,已知点Q(x,y)在抛物线上,点P(t,0)在x轴上.
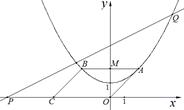
(1) 写出点M的坐标;
(2) 当四边形CMQP是以MQ,PC为腰的梯形时.
① 求t关于x的函数解析式和自变量x的取值范围;
② 当梯形CMQP的两底的长度之比为1:2时,求t的值.
定义[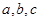 ]为函数
]为函数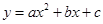 的特征数, 下面给出特征数为 [2m,1 – m , –1– m]
的特征数, 下面给出特征数为 [2m,1 – m , –1– m]
的函数的一些结论:
① 当m =" –" 3时,函数图象的顶点坐标是(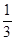 ,
,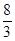 );
);
② 当m > 0时,函数图象截x轴所得的线段长度大于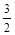 ;
;
③ 当m < 0时,函数在x >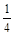 时,y随x的增大而减小;
时,y随x的增大而减小;
④ 当m¹ 0时,函数图象经过同一个点.
其中正确的结论有
| A.①②③④ | B.①②④ | C.①③④ | D.②④ |
已知抛物线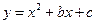 交x轴于A(1,0)、B(3,0)两点,交y轴于点C,其顶点为D.
交x轴于A(1,0)、B(3,0)两点,交y轴于点C,其顶点为D. 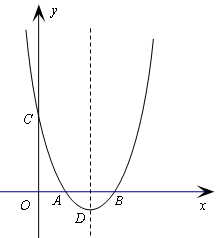
(1)求b、c的值并写出抛物线的对称轴;
(2)连接BC,过点O作直线OE⊥BC交抛物线的对称轴于点E.
求证:四边形ODBE是等腰梯形;
(3)抛物线上是否存在点Q,使得△OBQ的面积等于四边形ODBE的面积的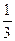 ?若存在,求点Q的坐标;若不存在,请说明理由.
?若存在,求点Q的坐标;若不存在,请说明理由.
如图,在矩形ABCD中, AB=4,BC=6,当直角三角板MPN 的直角顶点P在BC边上移动时,直角边MP始终经过点A,设直角三角板的另一直角边PN与CD相交于点Q.BP=x,CQ=y,那么y与x之间的函数图象大致是
已知二次函数 的图象C1与x轴有且只有一个公共点.
的图象C1与x轴有且只有一个公共点.
(1)求C1的顶点坐标;
(2)将C1向下平移若干个单位后,得抛物线C2,如果C2与x轴的一个交点为A(—3,0),求C2的函数关系式,并求C2与x轴的另一个交点坐标;
(3)若 的取值范围.
的取值范围.
如图5,
已知抛物线 的对称轴为
的对称轴为 ,点A,B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为
,点A,B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为
| A.(2,3) | B.(3,2) | C.(3,3) | D.(4,3) |
如图,平面直角坐标系中有一矩形ABCD(O为原点),点A、C分别在x轴、y轴上,且C点坐标为(0,6);将BCD沿BD折叠(D点在OC边上),使C点落在OA边的E点上,并将BAE沿BE折叠,恰好使点A落在BD的点F上.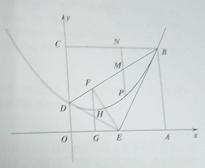
(1)直接写出∠ABE、∠CBD的度数,并求折痕BD所在直线的函数解析式;
(2)过F点作FG⊥x轴,垂足为G,FG的中点为H,若抛物线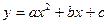 经过B、H、D三点,求抛物线的函数解析式;
经过B、H、D三点,求抛物线的函数解析式;
(3)若点P是矩形内部的点,且点P在(2)中的抛物线上运动(不含B、D点),过点P作PN⊥BC分别交BC和BD于点N、M,设h=PM-MN,试求出h与P点横坐标x的函数解析式,并画出该函数的简图,分别写出使PM<NM、PM=MN、PM>MN成立的x的取值范围。
如图1,抛物线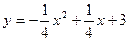 与x轴交于A、C两点,与y轴交于B点,与直线
与x轴交于A、C两点,与y轴交于B点,与直线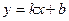 交于A、D两点。
交于A、D两点。
⑴直接写出A、C两点坐标和直线AD的解析式;
⑵如图2,质地均匀的正四面体骰子的各个面上依次标有数字-1、1、3、4.随机抛掷这枚骰子两次,把第一次着地一面的数字m记做P点的横坐标,第二次着地一面的数字n记做P点的纵坐标.则点 落在图1中抛物线与直线围成区域内(图中阴影部分,含边界)的概率是多少?
落在图1中抛物线与直线围成区域内(图中阴影部分,含边界)的概率是多少?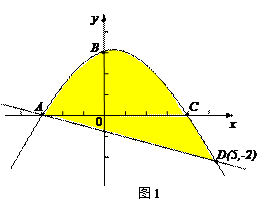

如图,在平面直角坐标系中,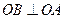 ,且
,且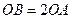 ,点
,点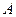 的坐标是
的坐标是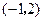 .
.
(1)求点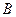 的坐标;
的坐标;
(2)求过点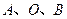 的抛物线的表达式;
的抛物线的表达式;
(3)连接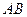 ,在(2)中的抛物线上求出点
,在(2)中的抛物线上求出点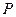 ,使得
,使得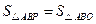 .
.
根据下表中的二次函数 的自变量
的自变量 与函数
与函数 的对应值,可判断该二次函数的图象与
的对应值,可判断该二次函数的图象与 轴( ).
轴( ).
 |
… |
 |
 |
 |
 |
… |
||||
 |
… |
 |
 |
 |
 |
…
|