2010年高级中等学校招生全国统一考试数学卷(浙江杭州)
有9名同学参加歌咏比赛,他们的预赛成绩各不相同,现取其中前4名参加决赛,小红同学在知道自己成绩的情况下,要判断自己能否进入决赛,还需要知道这9名同学成绩的
| A.众数 | B.中位数 | C.平均数 | D.极差 |
如图,在矩形ABCD中, AB=4,BC=6,当直角三角板MPN 的直角顶点P在BC边上移动时,直角边MP始终经过点A,设直角三角板的另一直角边PN与CD相交于点Q.BP=x,CQ=y,那么y与x之间的函数图象大致是
审计署发布公告:截止2010年5月20日,全国共接收玉树地震救灾捐赠款物70.44亿元.将70.44亿元用科学记数法表示为 ▲ 元.
在平面直角坐标系中,线段AB的端点A的坐标为(-3,2),将其先向右平移4个单位,再向下平移3个单位,得到线段A′B′,则点A对应点A′的坐标为 .
直线上有2010个点,我们进行如下操作:在每相邻两点间插入1个点,经过3次这样的操作后,直线上共有 ▲ 个点.
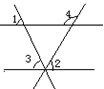
数学活动课上,老师在黑板上画直线平行于射线AN(如图),让同学们在直线l和射线AN上各找一点B和C,使得以A、B、C为顶点的三角形是等腰直角三角形.
这样的三角形最多能画 ▲ 个.
一家公司招考员工,每位考生要在A、B、C、D、E这5道试题中随机抽出2道题回答,规定答对其中1题即为合格.已知某位考生会答A、B两题,试求这位考生合格的概率.
如图,已知一次函数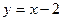 与反比例函数
与反比例函数 的图象交于A、B两点.
的图象交于A、B两点.
(1)求A、B两点的坐标;
(2)观察图象,可知一次函数值小于反比例函数值的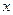 的取值范围是 ▲ .(把答案直接写在答题卡相应位置上)
的取值范围是 ▲ .(把答案直接写在答题卡相应位置上)
为了解学生课余活动情况,某校对参加绘画、书法、舞蹈、乐器这四个课外兴趣小组的人员分布情况进行抽样调查,并根据收集的数据绘制了下面两幅不完整的统计图,请根据图中提供的信息,解答下面的问题: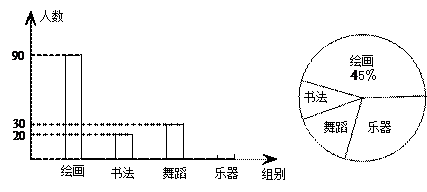
(1)此次共调查了多少名同学?
(2)将条形图补充完整,并计算扇形统计图中书法部分的圆心角的度数;
(3)如果该校共有1000名学生参加这4个课外兴趣小组,而每个教师最多只能辅导本组的20名学生,估计每个兴趣小组至少需要准备多少名教师?
如图,在平面直角坐标系中,O为原点,每个小方格的边长为1个单位长度.在第一象限内有横、纵坐标均为整数的A、B两点,且OA= OB= .
.
(1)写出A、B两点的坐标;
(2)画出线段AB绕点O旋转一周所形成的图形,并求其面积(结果保留π).
如图,AB是⊙O的直径, P为AB延长线上任意一点,C为半圆ACB的中点,PD切⊙O于点D,连结CD交AB于点E.
求证:(1)PD=PE;
(2)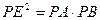 .
.
某花农培育甲种花木2株,乙种花木3株,共需成本1700元;培育甲种花木3株,乙种花木1株,共需成本1500元.
(1)求甲、乙两种花木每株成本分别为多少元?
(2)据市场调研,1株甲种花木售价为760元, 1株乙种花木售价为540元.该花农决定在成本不超过30000元的前提下培育甲乙两种花木,若培育乙种花木的株数是甲种花木的3倍还多10株,那么要使总利润不少于21600元,花农有哪几种具体的培育方案?
(本小题满分8分)
统计2010年上海世博会前20天日参观人数,得到如下频数分布表和频数分布 直方图(部分未完成):
|
| 组别(万人) |
组中值(万人) |
频数 |
频率 |
| 7.5~14.5 |
11 |
5 |
0.25 |
| 14.5~21.5 |
|
6 |
0.30 |
| 21.5~28.5 |
25 |
|
0.30 |
| 28.5~35.5 |
32 |
3 |
|
|

(1)请补全频数分布表和频数分布直方图;
(2)求出日参观人数不低于22万的天数和所占的百分比;
(3)利用以上信息,试估计上海世博会(会期184天)的参观总人数.
如图,在△ABC中,D、E两点分别在BC、AC边上.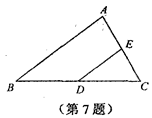
若BD=CD,∠B=∠CDE,DE=2,则AB的长度是
A.4 B.5 C.6 D.7
16位参加百米半决赛同学的成绩各不相同, 按成绩取前8位进入决赛. 如果小刘知道了自己的成绩后, 要判断能否进入决赛,其他15位同学成绩的下列数据中,能使他得出结论的是
| A.平均数 | B.极差 | C.中位数 | D.方差 |
如图,5个圆的圆心在同一条直线上, 且互相相切,若大圆直径是12,4个 
小圆大小相等,则这5个圆的周长的和为
| A.48π | B.24π | C.12π | D.6π |
如图,在△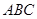 中,
中, 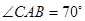 .
. 
在同一平面内, 将△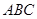 绕点A旋转到△
绕点A旋转到△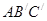 的位置, 使得
的位置, 使得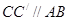 , 则
, 则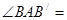
A.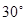 |
B. |
C.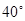 |
D.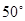 |
定义[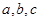 ]为函数
]为函数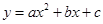 的特征数, 下面给出特征数为 [2m,1 – m , –1– m]
的特征数, 下面给出特征数为 [2m,1 – m , –1– m]
的函数的一些结论:
① 当m =" –" 3时,函数图象的顶点坐标是(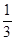 ,
,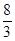 );
);
② 当m > 0时,函数图象截x轴所得的线段长度大于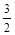 ;
;
③ 当m < 0时,函数在x >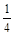 时,y随x的增大而减小;
时,y随x的增大而减小;
④ 当m¹ 0时,函数图象经过同一个点.
其中正确的结论有
| A.①②③④ | B.①②④ | C.①③④ | D.②④ |
一个密码箱的密码, 每个数位上的数都是从0到9的自然数, 若要使不知道密码的人一次就拨对密码的概率小于 , 则密码的位数至少需要 位.
, 则密码的位数至少需要 位.
如图, 已知△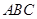 ,
,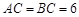 ,
,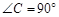 .
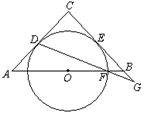
.
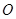 是
是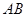 的中点,⊙
的中点,⊙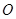 与AC,BC分别相切于点
与AC,BC分别相切于点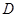 与点
与点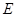 .点F是⊙
.点F是⊙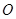 与
与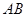 的一个交点,连
的一个交点,连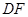 并延长交
并延长交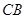 的延长线于点
的延长线于点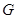 . 则
. 则 .
.
(本小题满分6分)
常用的确定物体位置的方法有两种. 
如图,在4×4个边长为1的正方形组成的方格中,标有A,B两点. 请你用两种不同方法表述点B相对点A的位置.
(本小题满分6分)
| (第18题) |
如图, 在平面直角坐标系 中, 点A(0,8), 点B(6 , 8 ).
中, 点A(0,8), 点B(6 , 8 ).
(1) 只用直尺(没有刻度)和圆规, 求作一个点P,使点P同时满足下
列两个条件(要求保留作图痕迹, 不必写出作法):
1)点P到A,B两点的距离相等;
2)点P到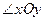 的两边的距离相等.
的两边的距离相等.
(2) 在(1)作出点P后, 写出点P的坐标.
(本小题满分6分)
给出下列命题:
命题1. 点(1,1)是直线y = x与双曲线y =  的一个交点;
的一个交点;
命题2. 点(2,4)是直线y = 2x与双曲线y =  的一个交点;
的一个交点;
命题3. 点(3,9)是直线y = 3x与双曲线y =  的一个交点;
的一个交点;
… … .
(1)请观察上面命题,猜想出命题 (
( 是正整数);
是正整数);
(2)证明你猜想的命题n是正确的.
(本小题满分8分)
已知直四棱柱的底面是边长为a的正方形, 高为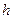 , 体积为V, 表面积等于S.
, 体积为V, 表面积等于S.
(1) 当a =" 2," h = 3时,分别求V和S;
(2) 当V = 12,S = 32时,求 的值.
的值.
(本小题满分10分)
如图,AB = 3AC,BD = 3AE,又BD∥AC,点B,A,E在同一条直线上.
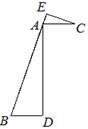
(1) 求证:△ABD∽△CAE;
(2) 如果AC =BD,AD = BD,设BD = a,求BC的长.
BD,设BD = a,求BC的长.
如图,台风中心位于点P,并沿东北方向PQ移动,已知台风移动的速度为30千米/时,受影响区域的半径为200千米,B市位于点P的北偏东75°方向上,距离点P 320千米处.
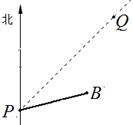
(1) 说明本次台风会影响B市;
(2)求这次台风影响B市的时间.




 m
m m
m ABC是一个圆锥的左视图,其中AB=AC=5,BC=8,则这个圆锥的侧面积是
ABC是一个圆锥的左视图,其中AB=AC=5,BC=8,则这个圆锥的侧面积是
 B.
B. C.
C. D.
D.
 = ▲ .
= ▲ . 的方程
的方程 的解,则
的解,则 的值为 ▲ .
的值为 ▲ . ,则
,则 = .
= . 等于 ▲ °.
等于 ▲ °.


 ,则
,则 的值为 ▲ .
的值为 ▲ .
 .
.
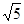
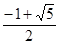
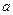 是实数,
是实数, 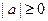 ”这一事件是
”这一事件是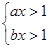
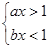
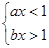
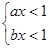
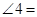 .
.
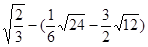 , 再求得它的近似值为 .(精确到0.01,
, 再求得它的近似值为 .(精确到0.01,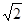 ≈1.414,
≈1.414,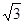 ≈1.732)
≈1.732)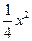 +1,点C的坐标为(–4,0),平行四边形OABC的顶点A,B在抛物线上,AB与y轴交于点M,已知点Q(x,y)在抛物线上,点P(t,0)在x轴上.
+1,点C的坐标为(–4,0),平行四边形OABC的顶点A,B在抛物线上,AB与y轴交于点M,已知点Q(x,y)在抛物线上,点P(t,0)在x轴上.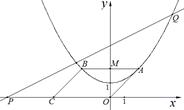
 粤公网安备 44130202000953号
粤公网安备 44130202000953号