对于抛物线y=ax2+bx+c(a≠0),有下列说法:
①当b=a+c时,则抛物线y=ax2+bx+c一定经过一个定点(-1,0);
②若△=b2-4ac>0,则抛物线y=cx2+bx+a与x轴必有两个不同的交点;
③若b=2a+3c,则抛物线y=ax2+bx+c与x轴必有两个不同的交点;
④若a>0,b>a+c,则抛物线y=ax2+bx+c与x轴必有两个不同的交点;
其中正确的有 .
如图,二次函数 的图象开口向上,图象经过点(-1,2)和(1,0),且与
的图象开口向上,图象经过点(-1,2)和(1,0),且与 轴相交于负半轴。则比较下列大小:①abc 0;②2a+b 0;③a+c 1;④a+b+c 0;⑤a 1。
轴相交于负半轴。则比较下列大小:①abc 0;②2a+b 0;③a+c 1;④a+b+c 0;⑤a 1。
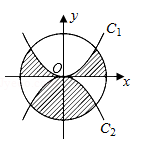
如图,⊙O的半径为2,C1是函数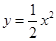 的图象,C2是函数
的图象,C2是函数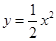 的图象,则阴影部分的面积是 .
的图象,则阴影部分的面积是 .
已知一个二次函数具有性质(1)图象不经过三、四象限;(2)点(2,1)在函数的图象上;(3)当x>0时,函数值y随自变量x的增大而增大.试写出一个满足以上性质的二次函数解析式: .
已知二次函数 (
( )的图象如图所示,给出以下结论:①
)的图象如图所示,给出以下结论:① ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤ .
.
其中结论正确的是 .(填正确结论的序号)

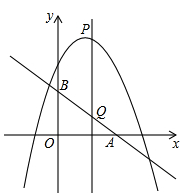
如图,已知直线y=- x+3分别交x轴、y轴于点A、B,P是抛物线y=-
x+3分别交x轴、y轴于点A、B,P是抛物线y=-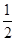 x2+2x+5上的一个动点,其横坐标为a,过点P且平行于y轴的直线交直线y=-
x2+2x+5上的一个动点,其横坐标为a,过点P且平行于y轴的直线交直线y=- x+3于点Q,则当PQ=BQ时,a的值是 .
x+3于点Q,则当PQ=BQ时,a的值是 .
如图,已知二次函数y=x2+bx+c的图像经过点(-1,0)、(1,-2),当y随x的增大而增大时,x的取值范围是 。
二次函数y=-2(x-5)2+3的开口方向 ;对称轴是直线 ;顶点坐标是 ;