山东省临沂市九年级上学期期中统考数学试卷
某经济开发区今年一月份工业产值达50亿元,第一季度总产值175亿元,问二、三月份平均每月增长率是多少?设平均每月增长率为百分之x,则( )
A. |
B. |
C. |
D. |
把抛物线 的图象向右平移3个单位,再向下平移2个单位,所得图象的解析式是
的图象向右平移3个单位,再向下平移2个单位,所得图象的解析式是 ,则有( )
,则有( )
| A.b=3,c=7 | B.b=-9,c=-15 | C.b=3,c=3 | D.b=-9,c=21 |
已知函数 的图象如图所示,那么关于x的方程
的图象如图所示,那么关于x的方程 的根的情况是( )
的根的情况是( )

| A.无实数根 |
| B.有两个相等实数根 |
| C.有两个异号实数 |
| D.有两个同号不等实数根 |
如图,A.B、C、D是⊙O上的三点,∠BAC=30°,则∠BOC的大小是( )

A.60° B.45° C.30° D.15°
如图,⊙O内切于△ABC,切点分别为D、E、F.已知∠B=50°,∠C=60°,连结OE,OF,DE,DF,那么∠EDF等于( )
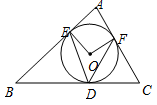
A.40° B.55° C.65° D.70°
已知二次函数 (
( )的图象如图所示,给出以下结论:①a+b+c<0;②a-b+c<0;③b+2a<0;④abc>0,其中所有正确结论的序号是( )
)的图象如图所示,给出以下结论:①a+b+c<0;②a-b+c<0;③b+2a<0;④abc>0,其中所有正确结论的序号是( )

| A.③④ | B.②③ | C.①④ | D.①②③ |
在△ABC 中,BC =4,以点A为圆心、2为半径的⊙A与BC相切于点D,交AB于E,交 AC于F,点P是⊙A上的一点,且∠EPF=40°,则图中阴影部分的面积是( )
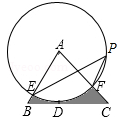
A.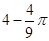 |
B.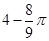 |
C.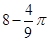 |
D.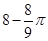 |
如图,若将△ABC绕点O顺时针旋转180°后得到△A′B′C′,则A点的对应点A′点的坐标是____________.
如图,一宽为2cm的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“2”和“8”(单位:cm),则该圆的半径为_____________cm.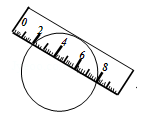
已知,如图:AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°.给出以下五个结论:①∠EBC=22.5°;②BD=DC;③AE=2EC;④劣弧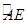 是劣弧
是劣弧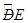 的2倍;⑤AE=BC.其中正确结论的序号是 .
的2倍;⑤AE=BC.其中正确结论的序号是 .
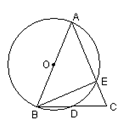
如图,在平面直角坐标系中,三角形②、③是由三角形①依次旋转后所得的图形.
(1)在图中标出旋转中心P的位置,并写出它的坐标;
(2)在图上画出再次旋转后的三角形④.
请同学们认真阅读下面的一段文字材料,然后解答题目中提出的有关问题.
为解方程 ,我们可以将
,我们可以将 视为一个整体,然后设
视为一个整体,然后设 ,则原方程可化为
,则原方程可化为 ①
①
解得 ,
, ,当y=1时,
,当y=1时, ,∴
,∴ ,
, ;
;
当y=4时, ,∴
,∴ ,
, ,∴原方程的解为
,∴原方程的解为 =
= ,
, =-
=- ,
, =
= ,
, =-
=- .
.
解答问题:
(1)填空:在由原方程得到方程①的过程中,利用_________法达到了降次的目的,体现了_________的数学思想.
(2)解方程 .
.
如果二次函数的二次项系数为l,则此二次函数可表示为 ,我们称[p,q]为此函数的特征数,如函数
,我们称[p,q]为此函数的特征数,如函数 的特征数是[2,3].
的特征数是[2,3].
(1)若一个函数的特征数为[﹣2,1],求此函数图象的顶点坐标.
(2)若一个函数的特征数为[4,﹣1],将此函数的图象先向右平移1个单位,再向上平移1个单位,求得到的图象对应的函数的特征数.
某工厂生产的某种产品按质量分为10个档次,第1档次(最低档次)的产品一天能生产95件,每件利润6元.每提高一个档次,每件利润增加2元,但一天产量减少5件.
(1)若生产第x档次的产品一天的总利润为y元(其中x为正整数,且1≤x≤10),求出y关于x的函数关系式;
(2)若生产第x档次的产品一天的总利润为1120元,求该产品的质量档次.
如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD,垂足为E,DA平分∠BDE.
(1)求证:AE是⊙O的切线;
(2)若∠DBC=30°,DE=1㎝,求BD的长.




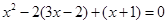 的一般形式是( )
的一般形式是( )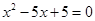
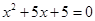
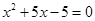

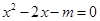 ,用配方法解该方程,配方后的方程为( )
,用配方法解该方程,配方后的方程为( )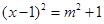
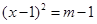
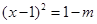
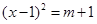
 是一元二次方程,则a=_________.
是一元二次方程,则a=_________. ,那么
,那么 的值为____________.
的值为____________.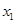 ,
,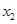 是方程
是方程 的两实数根,则
的两实数根,则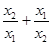 的值为____________.
的值为____________.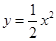 的图象,C2是函数
的图象,C2是函数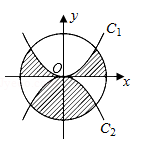
 的图象经过点(﹣1,4),且与直线
的图象经过点(﹣1,4),且与直线 相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x轴,垂足为点C(﹣3,0).
相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x轴,垂足为点C(﹣3,0).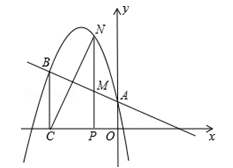
 粤公网安备 44130202000953号
粤公网安备 44130202000953号