河北省沙河市九年级上学期期末模拟考试数学试卷
已知方程(m-2) -2x+10=0是关于x的一元二次方程,则m的值为( )
-2x+10=0是关于x的一元二次方程,则m的值为( )
| A.2 | B.-2 | C.± |
D.±2 |
下列一元二次方程有两个不等的实数根的是
| A.(n-25)2=0 | B.y2+1=0 |
| C.x2+3x-5=0 | D.2m2+m=-1 |
函数 的图像经过点(2,8),则下列各点中不在图像
的图像经过点(2,8),则下列各点中不在图像 上的是( )
上的是( )
| A.(4,4) | B.(-4,-4) | C.(-2,8) | D.(8,2) |
已知抛物线 的开口向下,顶点坐标为(2,-3),那么该抛物线有( )
的开口向下,顶点坐标为(2,-3),那么该抛物线有( )
| A.最大值 -3 | B.最小值-3 | C.最小值2 | D.最大值2 |
一个密闭不透明的盒子里有若干个白球,在不许将球倒出来数的情况下,为估计白球数,小刚向其中放入8个黑球摇匀后,从中随意摸出一个球记下颜色,再把它放回盒中,不断重复这一过程,共摸球200次,其中44次摸到黑球,你估计盒中大约有白球( )
| A.20个 | B.28个 | C.36个 | D.无法估计 |
两圆的圆心坐标分别为(3,0)、(0,4),直径分别为4和6,则这两圆的位置关系是( )
| A.外离 | B.相交 | C.外切 | D.内切 |
如图为二次函数y=ax2-bx的图像,若一元二次方程ax2-bx+m=0有实数根,则m的最小值为( )
| A.8 | B.4 | C.-4 | D.-8 |
下列事件中的必然事件是( )
| A.天气阴了之后下雨 |
| B.小明上学路上看到两车相撞 |
| C.抛掷一枚骰子,朝上的一面点数恰好是5 |
| D.同时抛掷两枚骰子,朝上的两面点数之和小于13 |
如图,圆柱和球在同一水平面上紧靠在一起组成一个几何体,茗茗画出了它的三视图,其中所画的俯视图应该是( )
| A.两个外离的圆 | B.两个相交的圆 |
| C.两个外切的圆 | D.两个内切的圆 |
将抛物线y=2x2先向左平移一个单位,再向上平移一个单位,两次平移后得到的抛物线的解析式为( )
| A.y=2(x+1)2+1 | B.y=2(x+1)2-1 |
| C.y=2(x-1)2+1 | D.y=2(x-1)2-1 |
如图,Rt△ABC中,∠C=90°,AC=3,BC=4,若以A为旋转中心,将其按顺时针方向旋转60°到△AB'C'位置,则B点经过的路线长为( )
| A.π | B. π π |
C. π π |
D. π π |
如图,在梯形ABCD中,AD∥BC,∠BCD=90°,BC=2AD,F,E分别是AB,BC的中点,则下列结论不一定正确的是( )
| A.△ABC是等腰三角形 |
| B.四边形EFAM是菱形 |
C.S△BEF= S△ACD S△ACD |
| D.DE平分∠CDF |
如图,身高1.6m的小华站在距路灯5m的C点处,测得她在灯光下的影长CD为2.5m,则路灯的高度AB为 m.
如图为一个表面分别标有“A”“B”“C”“D”“E”“F”六个字母的正方体的平面展开图,则与字母“B”所在的面相对的面上标有字母“ ”。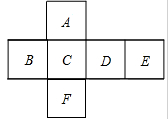
已知一个三角形最短边上的高为8cm,若和它相似的另一个三角形的各边之比为3:4:5,则它的最长边上的高为 cm.
如图,已知二次函数y=x2+bx+c的图像经过点(-1,0)、(1,-2),当y随x的增大而增大时,x的取值范围是 。
按要求解答下列各小题。
(1)计算:6cos60°-(sin21°-1)0×5tan45°;
(2)解方程:4x(3x-2)=6x-4.
如图,反比例函数 (k≠0)的图像过等边三角形AOB的顶点A,已知点B(-2,0)
(k≠0)的图像过等边三角形AOB的顶点A,已知点B(-2,0)
(1)求反比例函数的表达式;
(2)若要使点B在上述反比例函数的图像上,需将△AOB向上平移多少个单位长度?
如图,以线段AB为直径的⊙O交线段AC于点E,点D是AE的中点,连接OD并延长交⊙O于点M,∠BOE=60°,cosC= ,BC=
,BC= .
.
(1)求 的度数;
的度数;
(2)求证:BC是⊙ 的切线;
的切线;
(3)求弧AM的长度.
如图所示,二次函数y=-x2+2x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C。
(1)求m的值;
(2)求点B的坐标;
(3)该二次函数图像上有一点D(x,y)(其中x>0,y>0),使S△ABD=S△ABC,求点D的坐标。
如图,已知二次函数y=ax2+bx+2的图像经过A(-1,-1),C(1,3).
(1)求二次函数的解析式并画出它的图像;
(2)直接写出点A关于抛物线对称轴的对称点A'的坐标;
(3)求该抛物线上到x轴的距离为2的所有点的坐标。
为了落实国家的惠农政策,某地政府制定了农户投资购买收割机的补贴办法,其中购买Ⅰ、Ⅱ两型收割机所投资的金额与政府补贴的额度存在下表所示的函数对应关系:
| |
Ⅰ型收割机 |
|
Ⅱ型收割机 |
|
|
| 投资金额x(万元) |
x |
5 |
x |
2 |
4 |
| 补贴金额y(万元) |
y1=kx |
2 |
y2=ax2+bx |
2.4 |
3.2 |
(1)分别求出y1和y2的函数表达式;
(2)旺叔准备投资10万元购买Ⅰ、Ⅱ两型收割机。请你设计一个能获得最大补贴金额的方案,并求出按此方案能获得的补贴金额。
 中,x的取值范围是( )
中,x的取值范围是( )




 ,则sinA的值为( )
,则sinA的值为( )



 粤公网安备 44130202000953号
粤公网安备 44130202000953号