沙坪坝火车站将改造成一个集高铁、轻轨、公交、停车场、商业于一体的地下七层建筑,地面上欲建造一个圆形喷水池,如图, 点表示喷水池的水面中心,
点表示喷水池的水面中心,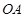 表示喷水柱子,水流从
表示喷水柱子,水流从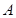 点喷出,按如图所示的直角坐标系,每一股水流在空中的路线可以用
点喷出,按如图所示的直角坐标系,每一股水流在空中的路线可以用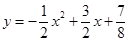 来描述,那么水池的半径至少要 米,才能使喷出的水流不致落到池外。
来描述,那么水池的半径至少要 米,才能使喷出的水流不致落到池外。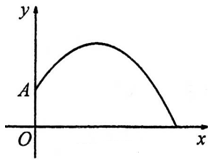
如图3,已知二次函数y1= ax2 + bx + c (a 0) 与一次函数y2=" kx" + m (k
0) 与一次函数y2=" kx" + m (k 0)的图象相交于点A (-2,4),B(8,2)(如图所示),则能使
0)的图象相交于点A (-2,4),B(8,2)(如图所示),则能使 成立的x的取值范围是 .
成立的x的取值范围是 .

一个二次函数解析式过点(3,1);当x>0时 y随x增大而减小;当x为2时函数值小于7,请写出符合要求的二次函数解析式______________
如图,双曲线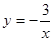 与抛物线
与抛物线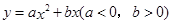 交于点P,P点的纵坐标为-1,则关于x的方程
交于点P,P点的纵坐标为-1,则关于x的方程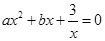 的解是 .
的解是 .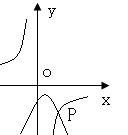
如图,已知直线y=- x+3分别交x轴、y轴于点A、B,P是抛物线y=-
x+3分别交x轴、y轴于点A、B,P是抛物线y=-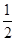 x2+2x+5上的一个动点,其横坐标为a,过点P且平行于y轴的直线交直线y=-
x2+2x+5上的一个动点,其横坐标为a,过点P且平行于y轴的直线交直线y=- x+3于点Q,则当PQ=BQ时,a的值是 .
x+3于点Q,则当PQ=BQ时,a的值是 .
把二次函数的表达式y=x2-4x+6化为y=a(x-h)2+k的形式,那么h+k= .
已知抛物线y=-x²+ mx+4的顶点为D, 它与x轴交于A和B两点,且A在原点左侧,B在原点右侧,与y轴的交点为P,且以AD为直径的圆M截y轴所得的弦EF恰好以点P为中点,则m的值为 .
抛物线y=x2-(b-2)x+3b 的顶点在y轴上,则b的值为 。
已知二次函数的顶点坐标为 ,并且经过平移后能与抛物线
,并且经过平移后能与抛物线 重合,那么这个二次函数的解析式是 .
重合,那么这个二次函数的解析式是 .