湖北省容城镇三闾学校九年级上学期期中考试数学试卷
下列函数不属于二次函数的是( )
| A.y=(x-1)(x+2) |
B.y=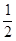 (x+1)2 (x+1)2 |
C.y=1-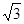 x2 x2 |
| D.y=2(x+3)2-2x2 |
下列关于x的方程中,一定是一元二次方程的为( )
| A.ax2+bx+c=0 | B.x2-2=(x+3)2 |
| C.2x+3 x −5=0 | D.x2-1=0 |
将一元二次方程5x2-1=4x化成一般形式后,一次项系数和二次项系数分别为( )
| A.5,-1 | B.5,4 | C.-4,5 | D.5x2,-4x |
抛物线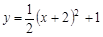 的顶点坐标是( )
的顶点坐标是( )
| A.(2,1) | B.(-2,1) | C.(2,-1) | D.(-2,-1) |
已知x=1是关于x的一元二次方程x2+mx-2=0的一个根,则m的值是( )
| A.-1 | B.0 | C.1 | D.0或1 |
若关于x的一元二次方程(k-1)x2+2x-2=0有实数根,则k的取值范围是( )
A.k> |
B.k≥ |
C.k> 且k≠1 且k≠1 |
D.k≥ 且k≠1 且k≠1 |
将抛物线y=3x2向左平移2个单位,再向下平移1个单位,所得抛物线为( )
| A.y=3(x-2)2-1 | B.y=3(x-2)2+1 |
| C.y=3(x+2)2-1 | D.y=3(x+2)2+1 |
二次函数y=ax2+bx+c(a≠0)的图象如图,下列结论正确的是( )
| A.a<0 | B.b2-4ac<0 | C.当-1<x<3时,y>0 | D.- ="1" ="1" |
在同一平面直角坐标系内,一次函数y=ax+b与二次函数y=ax2+8x+b的图象可能是( )
某商场要经营一种新上市的文具,进价为20元/件.试营销阶段发现:当销售单价是25元时,每天的销售量为250件;销售单价每上涨1元,每天的销售量就减少10件.已知每天所得的销售利润2000(元),设销售单价为x(元),则可列方程是;
| A.(25+x)(250-10x)-20(250-10x)=2000 |
| B.(250-10x)(5-x)=2000 |
| C.(x-20)[250-10 (x-20)]=2000 |
| D.(x-20)[250-10 (x-25)]=2000 |
某校九年级学生毕业时,每个同学都将自己的照片向全班其他同学各送了一张留作纪念,全班共送了2070张照片,如果全班有x名同学,则可列方程为 ,
如图所示,在同一坐标系中,作出①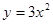 ②
②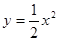 ③
③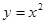 的图象,则图象从里到外的三条抛物线对应的函数依次是(填序号) 。
的图象,则图象从里到外的三条抛物线对应的函数依次是(填序号) 。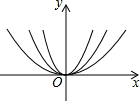
如图,E是正方形ABCD的边AB上的动点,EF⊥DE交BC于点F.若正方形的边长为4,AE=x,BF=y.则y与x的函数关系式为 ________ __.
若正数a是一元二次方程x2﹣5x+m=0的一个根,﹣a是一元二次方程x2+5x﹣m=0的一个根,则a的值是_____ .
已知关于x的方程mx2-(m+2)x+2=0(m≠0).
(1)求证:方程总有两个实数根;
(2)已知方程有两个不相等的实数根α,β满足 =1,求m的值.
=1,求m的值.
如图, 正方形ABCD的对角线相交于点 O,点O也是正方形A′B′C′O的一个顶点,如果两个正方形的边长都是2,求两个正方形重叠部分的面积。
已知关于x的方程x2+ax+a﹣2=0。
(1)若该方程的一个根为1,求a的值及该方程的另一根
(2)求证:不论a取何实数,该方程都有两个不相等的实数根.
已知抛物线与x轴相交于A(-1,0),B(3,0)两点,顶点坐标为C(1,4),
(1)求该抛物线解析式,
(2)判断开口方向以及增减情况
某工厂生产的某种产品按质量分为10个档次.第1档次(最低档次)的产品一天能生产76件,每件利润10元.每提高一个档次,每件利润增加2元,但一天产量减少4件.
(1)若生产第x档次的产品一天的总利润为y元(其中x为正整数,且1≤x≤10),求出y关于x的函数关系式;
(2)若生产第x档次的产品一天的总利润为1080元,求该产品的质量档次.
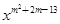 是二次函数,则m=______.
是二次函数,则m=______.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号