如图,直线y=-x+20与x轴、y轴分别交于A、B两点,动点P从A点开始在线段AO上以每秒3个长度单位的速度向原点O运动. 动直线EF从x轴开始以每秒1个长度单位的速度向上平行移动(即EF∥x轴),并且分别与y轴、线段AB交于E、F点. 连结FP,设动点P与动直线EF同时出发,运动时间为t秒.
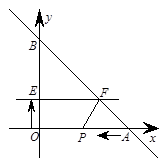
(1) 当t=1秒时,求梯形OPFE的面积;
(2) t为何值时,梯形OPFE的面积最大,最大面积是多少?
(3) 设t的值分别取t1、t2时(t1≠t2),所对应的三角形分别为△AF1P1和△AF2P2.试判断这两个三角形是否相似,请证明你的判断.