如图是抛物线y=ax2+bx+c的一部分,且其过点(3,0),对称轴为直线x=1,则下列结论正确的有 :

①abc>0
②方程ax2+bx+c=0有两个不相等的实数根
③a-b+c=0
④当x>0时,y随x的增大而增大
⑤不等式ax2+bx+c>0的解为x>3
⑥3a+2c<0.
已知二次函数y=-x2-2x+3的图象与x轴分别交于A、B两点(如图所示),与y轴交于点C,点P是其对称轴上一动点,当PB+PC取得最小值时,点P的坐标为 .

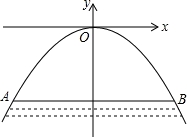
某桥洞是呈抛物线形状,它的截面在平面直角坐标系中如图所示,现测得水面宽AB=16m,桥洞顶点O到水面距离为16m,当水面上升7m时,水面宽为 m.
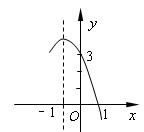
二次函数y=-x2+bx+c的部分图象如图所示,图象的对称轴为过点(-1,0)且平行于y轴的直线,图象与x轴交于点(1,0),则一元二次方程-x2+bx+c=0的根为 .
阅读材料,解答问题:
若两个二次函数图象的顶点,开口方向都相同,则称这两个二次函数为“同簇二次函数”.
(1)下列各组二次函数中,是“同簇二次函数”的是 (填序号);
①y=x2+1与y=2x2;
②y=x2+2x+2与y=2(x-1)2+1;
③y=-x2-2x+3与y=-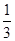 (x+1)2+4
(x+1)2+4
(2)已知关于x的二次函数y1=2x2-4mx+2m2+1和y2=ax2+bx+5,其中y1的图象经过点A(1,1),若y1+y2与y1为“同簇二次函数”,求函数y2的表达式.
已知二次函数y=x2-3x+m(m为常数)的图象与x轴的一个交点为(1,0),则关于x的一元二次方程x2-3x+m=0的两实数根是 .
二次函数 的图象如图,点A0位于坐标原点,点A1,A2,A3…An在y轴的正半轴上,点B1,B2,B3…Bn在二次函数位于第一象限的图象上,点C1,C2,C3…Cn在二次函数位于第二象限的图象上,四边形A0B1A1C1,四边形A1B2A2C2,四边形A2B3A3C3…四边形An﹣1BnAnCn都是菱形,∠A0B1A1=∠A1B2A1=∠A2B3A3…=∠An﹣1BnAn=60°,菱形An﹣1BnAnCn的周长为 .
的图象如图,点A0位于坐标原点,点A1,A2,A3…An在y轴的正半轴上,点B1,B2,B3…Bn在二次函数位于第一象限的图象上,点C1,C2,C3…Cn在二次函数位于第二象限的图象上,四边形A0B1A1C1,四边形A1B2A2C2,四边形A2B3A3C3…四边形An﹣1BnAnCn都是菱形,∠A0B1A1=∠A1B2A1=∠A2B3A3…=∠An﹣1BnAn=60°,菱形An﹣1BnAnCn的周长为 .

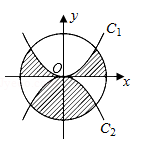
如图,⊙O的半径为2,C1是函数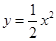 的图象,C2是函数
的图象,C2是函数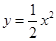 的图象,则阴影部分的面积是 .
的图象,则阴影部分的面积是 .
已知二次函数 (
( )的图象如图所示,给出以下结论:①
)的图象如图所示,给出以下结论:① ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤ .
.
其中结论正确的是 .(填正确结论的序号)
