初中数学二次函数在给定区间上的最值解答题

如图①所示，在直角梯形ABCD中，∠BAD=90°，E是直线AB上一点，过E作直线//BC，交直线CD于点F．将直线向右平移，设平移距离BE为 (t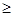0)，直角梯形ABCD被直线扫过的面积（图中阴影部份）为S，S关于的函数图象如图②所示，OM为线段，MN为抛物线的一部分，NQ为射线，N点横坐标为4．

信息读取
(1)梯形上底的长AB=     ；
(2) 直角梯形ABCD的面积=         ；
图象理解
(3)写出图②中射线NQ表示的实际意义；
(4) 当时，求S关于的函数关系式；
问题解决
(5)当t为何值时，直线l将直角梯形ABCD分成的两部分面积之比为1: 3．

已知：如图1，平面直角坐标系中，四边形OABC是矩形，点A，C的坐
标分别为（6，0），（0，2）．点D是线段BC上的一个动点（点D与点B，C不重合），过点D作直线＝－＋交折线O－A－B于点E．
（1）在点D运动的过程中，若△ODE的面积为S，求S与的函数关系式，并写出自变量的取值范围；
（2）如图2，当点E在线段OA上时，矩形OABC关于直线DE对称的图形为矩形O′A′B′C′，C′B′分别交CB，OA于点D，M，O′A′分别交CB，OA于点N，E．求证：四边形DMEN是菱形；
（3）问题（2）中的四边形DMEN中，ME的长为____________．

抛物线y=-x²+（m-1）x+m与y轴交于（0，3）点．
（1）求出m的值并在右图中画出这条抛物线．
（2）求它与x轴的交点和抛物线顶点的坐标．
（3）x取值什么值时，抛物线在x轴上方？
（4）x取什么值时，y的值随x的增大而减小？

已知抛物线(a≠0)的顶点在直线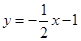上，且过点A(4，0)．
⑴求这个抛物线的解析式；
⑵设抛物线的顶点为P，是否在抛物线上存在一点B，使四边形OPAB为梯形？若存在，求出点B的坐标；若不存在，请说明理由.
⑶设点C(1，－3)，请在抛物线的对称轴确定一点D，使的值最大，请直接写出点D的坐标.

在平面直角坐标系中,已知二次函数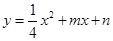的图象经过点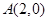和点,直线经过抛物线的顶点且与轴垂直,垂足为.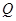
求该二次函数的表达式；
设抛物线上有一动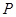点从点处出发沿抛物线向上运动,其纵坐标随时间
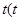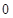≥)的变化规律为.现以线段为直径作.
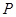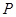①当点在起始位置点处时,试判断直线与的位置关系,并说明理由；在点运动的过程中,直线与是否始终保持这种位置关系? 请说明你的理由；
②若在点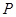开始运动的同时,直线也向上平行移动,且垂足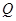的纵坐标随时间的变化规律为,则当在什么范围内变化时,直线与相交? 此时,若直线被所截得的弦长为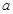,试求的最大值.

如图，直线y＝x－1和抛物线y＝x ²＋bx＋c都经过点A(1，0)，B(3，2)．
求抛物线的解析式；
求不等式x²＋bx＋c<x－1的解集（直接写出答案）．
设直线AB交抛物线对称轴与点D，请在对称轴上求一点P（D点除外），使△PBD为等腰三角形．（直接写出点P的坐标，不写过程

李明投资销售一种进价为20元的护眼台灯．销售过程中发现，每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数：y=－10x＋500．
⑴设李明每月获得利润为W(元)，当销售单价定为多少元时，每月获得利润最大？⑵如果李明想要每月获得2000元的利润，那么销售单价应定为多少元？
⑶根据物价部门规定，这种护眼台灯不得高于32元，如果李明想要每月获得的利润不低于2000元，那么他每月的成本最少需要多少元？（成本=进价×销售量）

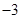   如图，在平面直角坐标系xOy中，一次函数 (为常数)的图象与x轴交于点A(，0)，与y轴交于点C．以直线x=1为对称轴的抛物线  ( 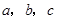为常数，且≠0)经过A，C两点，并与x轴的正半轴交于点B．
（1）求的值及抛物线的函数表达式；
（2）设E是y轴右侧抛物线上一点，过点E作直线AC的平行线交x轴于点F．是否存在这样的点E，使得以A，C，E，F为顶点的四边形是平行四边形？若存在，求出点E的坐标及相应的平行四边形的面积；若不存在，请说明理由；
（3）若P是抛物线对称轴上使△ACP的周长取得最小值的点，过点P任意作一条与y轴不平行的直线交抛物线于 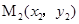，两点，试探究 是否为定值，并写出探究过程．

如图，已知抛物线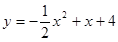交x轴的正半轴于点A，交y轴于点B.
求直线AB的解析式；
设P（x，y）（x>0）是直线y = x上的一点，Q是OP 的中点（O是原点），以PQ为对角线作正方形PEQF，若正方形PEQF与直线AB有公共点，求x的取值范围；
在（2）的条件下，记正方形PEQF与△OAB公共部分的面积为S，求S关于x的函数解析式，并探究S的最大值．

已知二次函数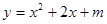的图象与x轴有且只有一个公共点.
求该二次函数的图象的顶点坐标；
若P(n，y₁)，Q（n+2，y₂）是该二次函数的图象上的两点，且y₁＞y₂，求实数n的取值范围.

如图，平面直角坐标系中，抛物线y＝－x²＋3x＋4与x轴交于点A、B（A在左侧），与y轴交于点C，抛物线的顶点为点M，对称轴与线段BC交于点N，点P为线段BC上一个动点(与B、C不重合) ．
求点A、B的坐标；
在抛物线的对称轴上找一点D，使|DC－DB|的值最大，求点D的坐标；
过点P作PQ∥y轴与抛物线交于点Q，连接QM，当四边形PQMN满足有一组对边相等时，求P点坐标．

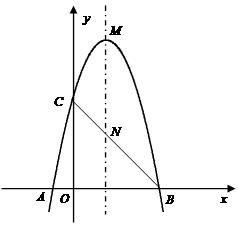
如图，抛物线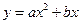（a0）与双曲线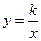相交于点A，B. 已知点A的坐标为（1，4），点B在第三象限内，且△AOB的面积为3（O为坐标原点）.

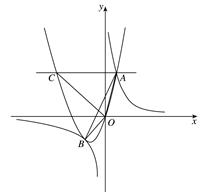
（1）求实数a，b，k的值；
（2）过抛物线上点A作直线AC∥x轴，交抛物线于另一点C，求所有满足△EOC∽△AOB的点E的坐标.