初中数学二次函数在给定区间上的最值解答题

如图，抛物线y=（x+m）²+m，与直线y=﹣x相交于E，C两点（点E在点C的左边），抛物线与x轴交于A，B两点（点A在点B的左边）．△ABC的外接圆⊙H与直线y=﹣x相交于点D．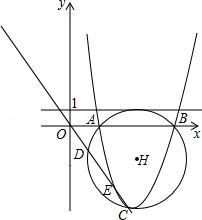

（1）若抛物线与y轴的交点坐标为（0，2），求m的值；
（2）求证：⊙H与直线y=1相切；
（3）若DE=2EC，求⊙H的半径．

抛物线与轴交于点A，B，与y轴交于点C，其中点B的坐标为.
（1）求抛物线对应的函数表达式；]
（2）将（1）中的抛物线沿对称轴向上平移，使其顶点M落在线段BC上，记该抛物线为G，求抛物线G所对应的函数表达式；
（3）将线段BC平移得到线段（B的对应点为，C的对应点为），使其经过（2）中所得抛物线G的顶点M，且与抛物线G另有一个交点N，求点到直线的距离的取值范围.

已知直角坐标系中菱形ABCD的位置如图所示，C．D两点的坐标分别为 （4，0）、（0，3）．现有两动点P、Q分别从A、C同时出发，点P沿线段AD向终点D运动，点Q沿折线CBA向终点A运动，设运动时间为ts．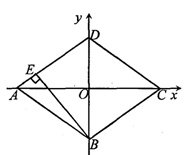

（1）菱形ABCD的边长是   ，面积是   ， 高BE的长是   ．（直接填写结果）
（2）探究下列问题：
①若点P的速度为1cm/s，点Q的速度为2 cm/s．当点Q在线段BA上时，求△APQ的面积S关于t的函数关系式，以及S的最大值；
②若点P的速度为1cm/s，点Q的速度变为kcm/s，在运动过程中，任何时刻都有相应的k值，使得△APQ沿它的一边翻折，翻折前后两个三角形组成的四边形为菱形，请探究当t＝4s时的情形，并求出k的值．

如图，点在抛物线上，过点作与轴平行的直线交抛物线于点，延长分别与抛物线相交于点，连接，设点的横坐标为，且。
当时，求点的坐标；
当为何值时，四边形的两条对角线互相垂直；
猜想线段与之间的数量关系，并证明你的结论．

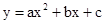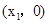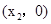在平面直角坐标系xOy中，已知二次函数的图象与x轴的正半轴交于A 、B两点（点A在点B的左侧），与y轴交于点C ．点A和点B间的距离为2， 若将二次函数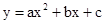的图象沿y轴向上平移3个单位时，则它恰好过原点，且与x轴两交点间的距离为4．
（1）求二次函数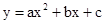的表达式；
（2）在二次函数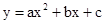的图象的对称轴上是否存在一点P，使点P到B、C两点距离之差最大？若存在，求出点P坐标；若不存在，请说明理由；
（3）设二次函数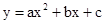的图象的顶点为D，在x轴上是否存在这样的点F，使得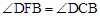？若存在，求出点F的坐标；若不存在，请说明理由．

如图，某建筑物的截面可以视作由两条线段AB，BC和一条曲线围成的封闭的平面图形．已知AB⊥BC，曲线是以点D为顶点的抛物线的一部分，BC=6m，点D到BC，AB的距离分别为4m和2m．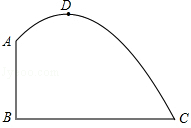

（1）请以BC所在直线为x轴（射线BC的方向为正方向），AB所在直线为y轴建立平面直角坐标系，求出抛物线的解析式，并直接写出自变量的取值范围；
（2）求AB的长．

如图，抛物线经过A、C（0，4）两点，与x轴的另一交点是B．
（1）求抛物线的解析式；
（2）若点在第一象限的抛物线上，求点D关于直线BC的对称点的坐标；
（3）在（2）的条件下，过点D作DE⊥BC于点E,反比例函数的图象经过点E，点在此反比例函数图象上，求的值．

（本小题满分8分）
已知抛物线y＝ax²＋bx＋6与x轴交于A、B两点（点A在原点的左侧，点B在原点的右侧），与y轴交于点C，且OB=OC，tan∠ACO=，顶点为D．
（1）求点A的坐标．
（2）求直线CD与x轴的交点E的坐标.
（3）在此抛物线上是否存在一点F，使得以点A、C、E、F为顶点的四边形是平行四边形？若存在，请求出点F的坐标；若不存在，请说明理由．
（4）若点M（2，y）是此抛物线上一点，点N是直线AM上方的抛物线上一动点，当点N运动到什么位置时，四边形ABMN的面积S最大? 请求出此时S的最大值和点N的坐标．
（5）点P为此抛物线对称轴上一动点，若以点P为圆心的圆与（4）中的直线AM及x轴同时相切，则此时点P的坐标为      .

已知，如图，抛物线y=ax²+3ax+c（a＞0）与y轴交于点C，与x轴交于A，B两点，点A在点B左侧．点B的坐标为（1，0），OC=3OB．

（1）求抛物线的解析式；
（2）若点D是线段AC下方抛物线上的动点，求四边形ABCD面积的最大值．

已知抛物线y=x²+bx+c过点（-6,-2），与y轴交于点C，且对称轴与x轴交于点B（-2,0），顶点为A.
（1）求该抛物线的解析式和A点坐标；
（2）若点D是该抛物线上的一个动点，且使△DBC是以B为直角顶点BC为腰的等腰直角三角形，求点D坐标；
（3）若点M是第二象限内该抛物线上的一个动点，经过点M的直线MN与y轴交于点N，是否存在以O、M、N为顶点的三角形与△OMB全等？若存在，请求出直线MN的解析式；若不存在，请说明理由．

已知抛物线经过点A（3，2），B（0，1）和点C．
（1）求抛物线的解析式；
（2）如图，若抛物线的顶点为P，点A关于对称轴的对称点为M，过M的直线交抛物线于另一点N（N在对称轴右边），交对称轴于F，若，求点F的坐标；
（3）在（2）的条件下，在y轴上是否存在点G，使△BMA与△MBG相似？若存在，求点G的坐标；若不存在，请说明理由．

如图，抛物线y=﹣x²+bx+c交x轴于点A，交y轴于点B，已知经过点A，B的直线的表达式为y=x+3．

（1）求抛物线的函数表达式及其顶点C的坐标；
（2）如图①，点P（m，0）是线段AO上的一个动点，其中﹣3＜m＜0，作直线DP⊥x轴，交直线AB于D，交抛物线于E，作EF∥x轴，交直线AB于点F，四边形DEFG为矩形．设矩形DEFG的周长为L，写出L与m的函数关系式，并求m为何值时周长L最大；
（3）如图②，在抛物线的对称轴上是否存在点Q，使点A，B，Q构成的三角形是以AB为腰的等腰三角形？若存在，直接写出所有符合条件的点Q的坐标；若不存在，请说明理由．

已知抛物线y=﹣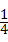x²+bx+c的对称轴为直线x=1,最小值为3，此抛物线与y轴交于点A，顶点为B，对称轴BC与x轴交于点C．
（1）求抛物线的解析式.
（2）如图1．求点A的坐标及线段OC的长；
（3）点P在抛物线上，直线PQ∥BC交x轴于点Q，连接BQ．
①若含45°角的直角三角板如图2所示放置．其中，一个顶点与点C重合，直角顶点D在BQ上，另一个顶点E在PQ上．求直线BQ的函数解析式；
②若含30°角的直角三角板一个顶点与点C重合，直角顶点D在直线BQ上，另一个顶点E在PQ上，求点P的坐标．

已知抛物线．
求抛物线顶点M的坐标；
若抛物线与x轴的交点分别为点A、B（点A在点B的左边），与y轴交于点C，点N为线段BM上的一点，过点N作x轴的垂线，垂足为点Q．当点N在线段BM上运动时（点N不与点B，点M重合），设NQ的长为t，四边形NQAC的面积为S，求S与t之间的函数关系式及自变量t的取值范围；
在对称轴右侧的抛物线上是否存在点P，使△PAC为直角三角形?若存在，求出所有符合条件的点P的坐标；若不存在，请说明理由．

已知二次函数．
求证：无论m为任何实数，该二次函数的图象与x轴都有两个交点；
当该二次函数的图象经过点（3，6）时，求二次函数的解析式；
将直线y=x向下平移2个单位长度后与（2）中的抛物线交于A、B两点（点A在点B的左边），一个动点P自A点出发，先到达抛物线的对称轴上的某点E，再到达x轴上的某点F，最后运动到点B．求使点P运动的总路径最短的点E、点F的坐标，并求出这个最短总路径的长．