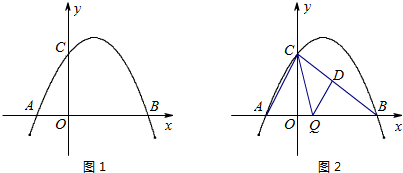初中数学二次函数在给定区间上的最值解答题

（本小题满分12分）已知某种水果的批发单价与批发量的函数关系如图1所示．
（1）请说明图中①、②两段函数图象的实际意义．
（2）写出批发该种水果的资金金额w（元）与批发量m（kg）之间的函数关系式；在上图的坐标系中画出该函数图象；指出金额在什么范围内，以同样的资金可以批发到较多数量的该种水果．
（3）经调查，某经销商销售该种水果的日最高销量与零售价之间的函数关系如图（2）所示，该经销商以每日售出60kg以上该种水果，且当日零售价不变，请你帮助该经销商设计进货和销售的方案，使得当日获得的利润最大．

如图，在平面直角坐标系中，已知点P（0，4），点A在线段OP上，点B在x轴正半轴上，且AP=OB=t， 0＜t＜4，以AB为边在第一象限内作正方形ABCD；过点C、D依次向x轴、y轴作垂线，垂足为M，N，设过O，C两点的抛物线为y=ax²+bx+c．
（1）填空：△AOB≌△       ≌△BMC（不需证明）；用含t的代数式表示A点纵坐标：A（0，       ；
（2）求点C的坐标，并用含a，t的代数式表示b；
（3）当t=1时，连接OD，若此时抛物线与线段OD只有唯一的公共点O，求a的取值范围；
（4）当抛物线开口向上，对称轴是直线，顶点随着t的增大向上移动时，求t的取值范围．

如图，⊙M与x轴交于A、B两点，其坐标分别为、，直径CD⊥x轴于N，抛物线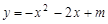经过A、B、D三点，
(1)求m的值及点D的坐标.
(2)若直线CE切⊙M于点C，G在直线CE上，已知点G的横坐标为3.求G的纵坐标
(3)对于(2)中的G，是否存在过点G的直线，使它与（1）中抛物线只有一个交点，请说明理由.
(4)对于(2)中的G直线FG切⊙M于点F，求直线DF的解析式.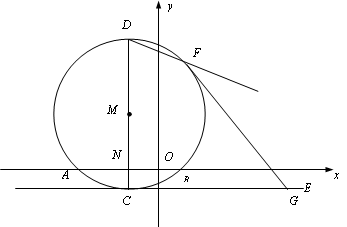

某商店经营一种成本为每千克40美元的水产品，根据市场分析，若按每千克50元销售，一个月能售出500千克；销售价每涨1元，月销售量就减少10千克，
(1)针对这种水产品的销售情况，设销售单价定为x元(x>50)，请用的x代数式表示月销售量,以及获得的利润.
(2)当x取什么数时利润最大?最大利润是多少？

如图，抛物线y=﹣x²+3x+4与x轴交于A、B两点，与y轴交于C点，点D在抛物线上且横坐标为3．
（1）求tan∠DBC的值；
（2）点P为抛物线上一点，且∠DBP=45°，求点P的坐标．

（本小题12分）已知抛物线p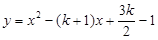：和直线l:：
（1）对下列命题判断真伪，并说明理由：
①无论k取何实数值，抛物线p总与x轴有两个不同的交点；
②无论k取何实数值，直线l与y轴的负半轴没有交点；
（2）设抛物线p与y轴交点为C，与x轴的交点为A、B，原点O不在线段AB上；直线l与x轴的交点为D，与y轴交点为C₁，当OC₁＝OC＋2且OD²＝4AB²时，求出抛物线的解析式及最小值.

如图，在平面直角坐标系中，抛物线y=ax²+bx+4与x轴的一个交点为A（-2，0），与y轴的交点为C，对称轴是x=3，对称轴与x轴交于点B．
（1）求抛物线的函数表达式；
（2）经过B，C的直线l平移后与抛物线交于点M，与x轴交于点N，当以B，C，M，N为顶点的四边形是平行四边形时，求出点M的坐标；
（3）若点D在x轴上，在抛物线上是否存在点P，使得△PBD≌△PBC？若存在，直接写出点P的坐标；若不存在，请说明理由．

抛物线y=+x+m的顶点在直线y=x+3上，过点F（﹣2，2）的直线交该抛物线于点M、N两点（点M在点N的左边），MA⊥x轴于点A，NB⊥x轴于点B．

（1）先通过配方求抛物线的顶点坐标（坐标可用含m的代数式表示），再求m的值；
（2）设点N的横坐标为a，试用含a的代数式表示点N的纵坐标，并说明NF=NB；
（3）若射线NM交x轴于点P，且PA•PB=，求点M的坐标．

如图,在平面直角坐标系中，⊙O的圆心在坐标原点,半径为3．过A（-7，9），B（0，9）的抛物线（a,b,c为常数，且a≠0）与x轴交于D，E （点D在点E右边）两点,连结AD．

（1）若点D的坐标为D（3，0）．①请直接写出此时直线AD与⊙O的位置关系；②求此时抛物线对应的函数关系式；
（2）若直线AD和⊙O相切,求抛物线二次项系数a的值；
（3）当直线AD和⊙O相交时,直接写出a的取值范围．

如图，抛物线C₁：y=（x+m）²（m为常数，m＞0），平移抛物线y=﹣x²，使其顶点D在抛物线C₁位于y轴右侧的图象上，得到抛物线C₂．抛物线C₂交x轴于A，B两点（点A在点B的左侧），交y轴于点C，设点D的横坐标为a．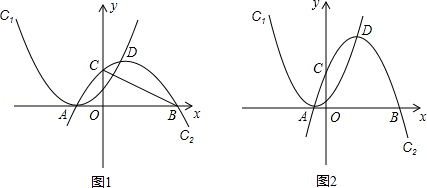

（1）如图1，若m=．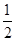
①当OC=2时，求抛物线C₂的解析式；
②是否存在a，使得线段BC上有一点P，满足点B与点C到直线OP的距离之和最大且AP=BP？若存在，求出a的值；若不存在，请说明理由；
（2）如图2，当OB=2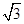﹣m（0＜m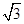＜）时，请直接写出到△ABD的三边所在直线的距离相等的所有点的坐标（用含m的式子表示）．

如图，已知二次函数的图象与坐标轴交于点A（-1， 0）和点

B（0，-5）．
（1）求该二次函数的解析式；
（2）已知该函数图象的对称轴上存在一点P，使得△ABP的周长最小．请求出点P的坐标．

在平面直角坐标系中，抛物线经过点（0，），（3，4）．
（1）求抛物线的表达式及对称轴；
（2）设点关于原点的对称点为，点是抛物线对称轴上一动点，记抛物线在，之间的部分为图象（包含，两点）．若直线与图象有公共点，结合函数图像，求点纵坐标的取值范围．

如图,抛物线经过点A(1,0)和点P(3,4).
求此抛物线的解析式,写出抛物线与x轴的交点坐标和顶点坐标,并依此在所给平面直角坐标系中画出抛物线的大致图象;
若抛物线与轴的另一个交点为B,现将抛物线向射线AP方向平移,使P点落在M点处,同时抛物线上的B点落在点D（BD∥PM）处.设抛物线平移前P、B之间的曲线部分与平移后M、D之间的曲线部分，与线段MP、BD所围成的面积为m, 线段 PM为n,求m与n的函数关系式.

如图，在平面直角坐标系中，A是抛物线y=x²上的一个动点，且点A在第一象限内．AE⊥y轴于点E，点B坐标为（0，6），直线AB交x轴于点C，点D与点C关于y轴对称，直线DE与AB相交于点F，连结BD．设线段AE的长为a，△BED的面积为S．

（1）当a=时，求S的值．
（2）求S关于a（a≠）的函数解析式．

己知：二次函数y=ax²+bx+6（a≠0）与x轴交于A、B两点（点A在点B的左侧）点
A、点B的横坐标是一元二次方程x²-4x-12=0的两个根．
（1）请直接写出点A、点B的坐标．
（2）请求出该二次函数表达式及对称轴和顶点坐标．
（3）如图1，在二次函数对称轴上是否存在点P，使△APC的周长最小，若存在，请求出点P的坐标；若不存在，请说明理由．
（4）如图2，连接AC、BC，点Q是线段0B上一个动点（点Q不与点0、B重合）．过点Q作QD∥AC交BC于点D，设Q点坐标（m，0），当△CDQ面积S最大时，求m的值．