初中数学二次函数在给定区间上的最值解答题

在平面直角坐标系中，已知抛物线（a，c为常数）的顶点为P，等腰直角三角形ABC的顶点A的坐标为（0，﹣1），C的坐标为（﹣4，3），直角顶点B在第二象限．
（1）如图，若该抛物线过A，B两点，求该抛物线的函数表达式；

（2）平移（1）中的抛物线，使顶点P在直线AC上滑动，且与AC交于另一点Q，判断线段PQ的长度是否为定值？如果是，求出PQ的长；如果不是，说明理由；
（3）在（2）的条件下，若点M在直线AC下方，且为平移前（1）中的抛物线上的点，以M、P、Q三点为顶点的三角形是等腰直角三角形，求出所有符合条件的点M的坐标．

复习课中，教师给出关于x的函数（k是实数）.
教师：请独立思考，并把探索发现的与该函数有关的结论（性质）写到黑板上.
学生思考后，黑板上出现了一些结论.教师作为活动一员，又补充一些结论，并从中选择如下四条：
①存在函数，其图像经过（1,0）点；
②函数图像与坐标轴总有三个不同的交点；
③当时，不是y随x的增大而增大就是y随x的增大而减小；
④若函数有最大值，则最大值必为正数，若函数有最小值，则最小值必为负数；
教师：请你分别判断四条结论的真假，并给出理由，最后简单写出解决问题时所用的数学方法.

如图，抛物线y=x²+bx+c与直线y=x－1交于A、B两点.点A的横坐标为－3，点B在y轴上，点P是y轴左侧抛物线上的一动点，横坐标为m，过点P作PC⊥x轴于C，交直线AB于D.
（1）求抛物线的解析式；
（2）当m为何值时，；
（3）是否存在点P,使△PAD是直角三角形，若存在，求出点P的坐标；若不存在，说明理由.

如图，三角形ABC是以BC为底边的等腰三角形，点A、C分别是一次函数y=-x+3的图象与y轴、x轴的交点，点B在二次函数的图象上，且该二次函数图象上存在一点D使四边形ABCD能构成平行四边形．

（1）试求b，c的值，并写出该二次函数表达式；
（2）动点P从A到D，同时动点Q从C到A都以每秒1个单位的速度运动，问：
①当P运动到何处时，有PQ⊥AC？
②当P运动到何处时，四边形PDCQ的面积最小？此时四边形PDCQ的面积是多少？

已知在平面直角坐标系中，抛物线y=ax²+bx+c（a≠0，且a，b，c为常数）的对称轴为：直线x=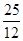，与x轴分别交于点A、点B，与y轴交于点C（0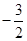，），且过点（3，-5），D为x轴正半轴上的动点，E为y轴负半轴上的动点．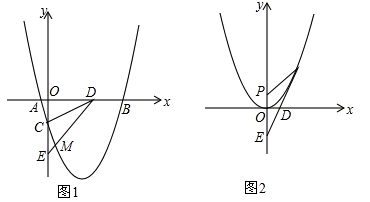

（1）求该抛物线的表达式；
（2）如图1，当点D为（3，0）时，DE交该抛物线于点M，若∠ADC=∠CDM，求点M的坐标；
（3）如图2，把（1）中抛物线平移使其顶点与原点重合，若直线ED与新抛物线仅有唯一交点Q时，y轴上是否存在一个定点P使PE=PQ？若存在，求出点P的坐标；若不存在，请说明理由．

如图，抛物线与x轴交于A（5,0）、B（-1,0）两点，过点A作直线AC⊥x轴，交直线于点C；
（1）求该抛物线的解析式；
（2）求点A关于直线的对称点的坐标，判定点是否在抛物线上，并说明理由；
（3）点P是抛物线上一动点，过点P作y轴的平行线，交线段于点M，是否存在这样的点P，使四边形PACM是平行四边形？若存在，求出点P的坐标；若不存在，请说明理由.

如图，矩形ABCD中，AB=20，BC=10，点P为AB边上一动点，DP交AC于点Q.
（1）求证：△APQ∽△CDQ；
（2）P点从A点出发沿AB边以每秒1个单位的速度向B点移动，移动时间为t秒.
①当t为何值时，DP⊥AC？
②设，写出y与t之间的函数解析式，并探究P点运动到第几秒到第几秒之间时，y取得最小值.

某商店经营一种小商品，进价为每件20元，据市场分析，在一个月内，售价定为25元时，可卖出105件，而售价每上涨1元，就少卖5件．
（1）当售价定为30元时，一个月可获利多少元？
（2）当售价定为每件多少元时，一个月的获利最大？最大利润是多少元？

为了落实国务院的指示精神，某地方政府出台了一系列“三农”优惠政策，使农民收入大幅度增加．某农户生产经销一种农产品，已知这种产品的成本价为每千克20元，市场调查发现，该产品每天的销售量y（千克）与销售价x（元/千克）有如下关系：y＝－2x＋80．设这种产品每天的销售利润为w元．
（1）求w与x之间的函数关系式；
（2）该产品销售价定为每千克多少元时，每天的销售利润最大？最大是多少元？
（3）如果物价部门规定这种产品的销售价不高于每千克28元，该农户想要每天获得150元的销售利润，销售价应定为每千克多少元？                         

已知：二次函数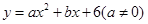与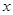轴交于A，B两点（点A在点B的左侧），点A、点B的横坐标是一元二次方程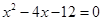的两个根．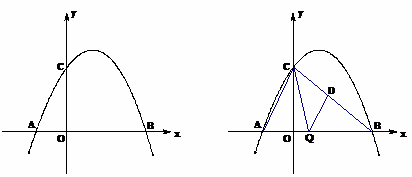

（1）请直接写出点A、B的坐标，并求出该二次函数的解析式。
（2）如图1，在二次函数对称轴上是否存在点P，使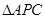的周长最小，若存在，请求出点P的坐标；若不存在，请说明理由．
（3）如图2，连接AC、BC，点Q是线段OB上一个动点（点Q不与点O、B重合）．过点Q作QD∥AC交于BC点D，设Q点坐标（m，0），当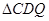面积S最大时，求m的值．

如图，已知抛物线的顶点坐标为M（1,4），且经过点N（2,3），与x轴交于A、B两点（点A在点B左侧），与y轴交于点C。

（1）点A、B、C的坐标分别为        、        、        。
（2）若直线y=kx+t经过C、M两点，且与x轴交于点D，试证明四边形CDAN是平行四边形；
（3）点P在抛物线的对称轴x=1上运动，请探索：在x轴上方是否存在这样的P点，使以P为圆心的圆经过A、B两点，并且与直线CD相切，若存在，请求出点P的坐标；若不存在，请说明理由。

(14分)已知抛物线y＝ax2＋bx＋c(a≠0)经过A(－2，0)、B(0，1)两点，且对称轴是y轴．经过点C(0，2)的直线l与x轴平行，O为坐标原点，P、Q为抛物线y＝ax2＋bx＋c(a≠0)上的两动点．

(1) 求抛物线的解析式；
(2) 以点P为圆心，PO为半径的圆记为⊙P，判断直线l与⊙P的位置关系，并证明你的结论；
(3) 设线段PQ＝9，G是PQ的中点，求点G到直线l距离的最小值．

（本小题满分14分）
如图所示，抛物线经过原点，与轴交于另一点,直线与两坐标轴分别交于、两点，与抛物线交于、两点.

（1）求直线与抛物线的解析式；
（2）若抛物线在轴上方的部分有一动点，
求的面积最大值；
（3）若动点保持（2）中的运动路线，问是否存在点
，使得的面积等于面积的？若存在，请求出点的坐标；
若不存在，请说明理由．

（本小题满分7分）如图，已知二次函数的图象与x轴负半轴交于点A（-1，0），与y轴正半轴交与点B，顶点为P，且OB=3OA，一次函数y=kx+b的图象经过A、B．

（1）求一次函数解析式；
（2）求顶点P的坐标；
（3）平移直线AB使其过点P，如果点Ｍ在平移后的直线上，且，求点M坐标；
（４）设抛物线的对称轴交x轴与点E，联结AP交y轴与点D，若点Q、N分别为两线段PE、PD上的动点，联结QD、QN，请直接写出QD+QN的最小值．

（本小题满分10分）已知直线y=x＋4与x轴，y轴分别交于A、B两点，∠ABC=60°，BC与x轴交于点C.
（1）试确定直线BC的解析式.
（2）若动点P从A点出发沿AC向点C运动（不与A、C重合），同时动点Q从C点出发
沿CBA向点A运动(不与C、A重合) ，动点P的运动速度是每秒1个单位长度，动点Q
的运动速度是每秒2个单位长度.设△APQ的面积为S，P点的运动时间为t秒，求S与t的
函数关系式，并写出自变量的取值范围.
（3）在（2）的条件下，当△APQ的面积最大时，y轴上有一点M，平面内是否存在一点
N，使以A、Q、M、N为顶点的四边形为菱形？若存在，请直接写出N点的坐标；若不存
在，请说明理由.