广东省汕头市潮南区初中毕业生学业考试数学试卷
据有关专家统计,国家“一带一路”战略将产生21万亿美元的经济效应。数字21万亿科学计数法可表示为( )
A. |
B. |
C. |
D. |
为了解某社区居民的用电情况,随机对该社区10户居民进行了调查,下表是这10户居民2015年3月份用电量的调查结果如表所示,那么关于这10户居民月用电量(单位:度),下列说法错误的是( )
| 月用电量(度/户) |
40 |
50 |
55 |
60 |
| 居民(户) |
1 |
3 |
2 |
4 |
A.中位数是55 B.众数是60
C.方差是29 D.平均数是54
从左到右的变形,是因式分解的为 ( )
| A.(3﹣x)(3+x)=9﹣x2 |
| B.(a-b)(a2+ab+b2)=a3-b3 |
| C.a2-4ab+4b2-1=a(a-4b)+(2b+1)(2b-1) |
| D.4x2-25y2=(2x+5y)(2x-5y) |
已知一次函数y=kx+k-1和反比例函数y= ,则这两个函数在同一平面直角坐标系中的图象不可能是( )
,则这两个函数在同一平面直角坐标系中的图象不可能是( )
如图,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD对折,点C落在点C′的位置,BC′交AD于点G.则△BDG的面积的值是( )
| A.18.75cm2 | B.19.15 cm2 | C.20 cm2 | D.21.35 cm2 |
如图,在菱形ABCD中,∠A=60º,E、F分别是AB、AD的中点,若EF=2,则菱形ABCD的边长是_______ .

如图,AB是⊙O的直径,点D在AB的延长线上,DC切⊙O于C, 若∠A=25º则∠D等于___________.

如图,⊙O中,半径OA=4,∠AOB=120°,用阴影部分的扇形围成的圆锥底面圆的半径长是___________ .
如图所示,如果以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以AE为边作第三个正方形AEGM,…已知正方形ABCD的面积S1=1,按上述方法所作的正方形的面积依次为S2,S3,…Sn(n为正整数),那么第8个正方形面积S8= .
如图,方格纸中的每个小正方形边长都是1个单位长度,Rt△ABC的顶点均在格点上.建立平面直角坐标系后,点A的坐标为(1,1),点B的坐标为(4,1).
(1)先将Rt△ABC向左平移5个单位长度,再向下平移1个单位长度得到Rt△A1B1C1,试在图中画出Rt△A1B1C1,并写出点A1的坐标;
(2)再将Rt△A1B1C1绕点A1顺时针旋转90°后得到Rt△A1B2C2,试在图中画出Rt△A1B2C2,并计算Rt△A1B1C1在上述旋转过程点C1所经过的路径长.
如图,某幢大楼顶部有一块广告牌CD,甲乙两人分别在相距8米的A、B两处测得D点和C点的仰角分别为45°和60°,且A、B、E三点在一条直线上,若BE=15米,求这块广告牌的高度.(取 ≈1.73,计算结果保留整数)
≈1.73,计算结果保留整数) 
六·一”儿童节前夕,某童装专卖店用2500元购进一批儿童服装,上市后很快脱销,接着又用4500元购进第二批这种服装,所购数量是第一批数量的1.5倍,但每套进价多了10元.
(1)求第一批童装每套的进价是多少元?
(2)如果这两批童装每套售价相同,且全部售完后总利润不低于25%,那么每套售价至少是多少元?
甲口袋中装有两个相同的小球,它们的标号分别为2和7,乙口袋中装有两个相同的小球,它们的标号分别为4和5,丙口袋中装有三个相同的小球,它们的标号分别为3,8,9.从这3个口袋中各随机地取出1个小球.
(1)求取出的3个小球的标号全是奇数的概率是多少?
(2)以取出的三个小球的标号分别表示三条线段的长度,求这些线段能构成三角形的概率.
如图,一次函数y=kx+b与反比例函数 的图象交于A(m,6),B(3,n)两点.
的图象交于A(m,6),B(3,n)两点.
(1)求一次函数的解析式;
(2)根据图象直接写出 的x的取值范围;
的x的取值范围;
(3)求△AOB的面积.
如图所示,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.
(1)求证:BC是⊙O的切线;
(2)连接AF,BF,求∠ABF的度数;
(3)如果CD=15,BE=10,sinA= ,求⊙O的半径
,求⊙O的半径
 | 的倒数是( )
| 的倒数是( )
 =
= 2
2 =2
=2

 的一元二次方程
的一元二次方程 有两个不相等的实数根,则
有两个不相等的实数根,则 的取值范围是( )
的取值范围是( )


 ,其解集为_________________ .
,其解集为_________________ . ,则以x,y的值为两边长的等腰三角形的周长是 .
,则以x,y的值为两边长的等腰三角形的周长是 .
 ,其中a= -1
,其中a= -1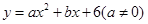 与
与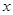 轴交于A,B两点(点A在点B的左侧),点A、点B的横坐标是一元二次方程
轴交于A,B两点(点A在点B的左侧),点A、点B的横坐标是一元二次方程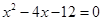 的两个根.
的两个根.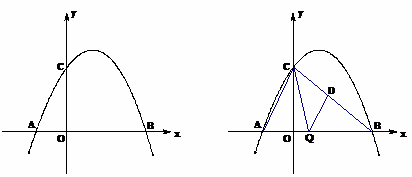
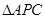 的周长最小,若存在,请求出点P的坐标;若不存在,请说明理由.
的周长最小,若存在,请求出点P的坐标;若不存在,请说明理由.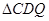 面积S最大时,求m的值.
面积S最大时,求m的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号