初中数学二次函数在给定区间上的最值解答题

设函数（k是常数）．
（1）当k=1和k=2时的函数和的图像如图所示，请你在同一坐标系中画出k=3时函数的图像；

（2）根据图像，写出你发现的两条结论；
（3）将函数的图像向左平移2个单位，再向下平移4个单位，得到函数的图像。请写出函数的解析式，回答自变量x取何值时，函数的最小值是多少？

如图，抛物线y=ax²+bx+3经过A（-1，0），B（3，0）两点，且交y轴于点C，对称轴与抛物线相交于点P、与直线BC相交于点M．

（1）求该抛物线的解析式．
（2）在抛物线上是否存在一点N，使得|MN-ON|的值最大？若存在，请求出点N的坐标；若不存在，请说明理由．
（3）连接PB，请探究：在抛物线上是否存在一点Q，使得△QMB与△PMB的面积相等？若存在，求出点Q的坐标；若不存在，请说明理由．

如图，已知抛物线y=-ax²+2ax+3a（a≠0）与x轴交于A、B两点，与y轴交于点C．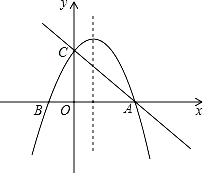

（1）请直接写出A、B两点的坐标．
（2）当a=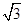，设直线AC与抛物线的对称轴交于点P，请求出△ABP的面积．

如图，已知二次函数L₁:y=ax²-2ax+a+3（a＞0）和二次函数L₂:y=-a（x+1）²+1（a＞0）图象的顶点分别为M，N ， 与轴分别交于点E， F．

（1） 函数的最小值为             ；
当二次函数L₁ ，L₂的值同时随着的增大而减小时，的取值范围是                ；
（2）当时，求的值，并判断四边形的形状（直接写出，不必证明）；
（3）若二次函数L₂的图象与轴的右交点为，当△为等腰三角形时，求方程的解．

九（1）班数学兴趣小组经过市场调查，整理出某种商品在第（1≤≤90）天的售价与销量的相关信息如下表：

时间x（天）	1≤x＜50	50≤x≤90
售价（元/件）	x+40	90
每天销量（件）	200﹣2x

已知该商品的进价为每件30元，设销售该商品的每天利润为元．
（1）求出与的函数关系式；
（2）问销售该商品第几天时，当天销售利润最大，最大利润是多少？
（3）该商品在销售过程中，共有多少天每天销售利润不低于4800元？请直接写出结果．

抛物线y=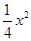+x+m的顶点在直线y=x+3上，过点F（-2，2）的直线交该抛物线于点M、N两点（点M在点N的左边），MA⊥x轴于点A，NB⊥x轴于点B．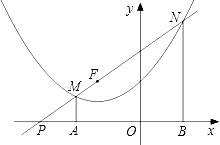

（1）先通过配方求抛物线的顶点坐标（坐标可用含m的代数式表示），再求m的值；
（2）设点N的横坐标为a，试用含a的代数式表示点N的纵坐标，并说明NF=NB；
（3）若射线NM交x轴于点P，且PA•PB=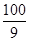，求点M的坐标．

如图，抛物线y=ax²+bx+3经过A（﹣1，0），B（3，0）两点，且交y轴于点C，对称轴与抛物线相交于点P、与直线BC相交于点M．

（1）求该抛物线的解析式．
（2）在抛物线上是否存在一点N，使得|MN﹣ON|的值最大？若存在，请求出点N的坐标；若不存在，请说明理由．
（3）连接PB，请探究：在抛物线上是否存在一点Q，使得△QMB与△PMB的面积相等？若存在，求出点Q的坐标；若不存在，请说明理由．

为了节省材料，某水产养殖户利用水库的岸堤（岸堤足够长）为一边，用总长为80m的围网在水库中围成了如图所示的①②③三块矩形区域，而且这三块矩形区域的面积相等．设BC的长度为xm，矩形区域ABCD的面积为ym²．

（1）求y与x之间的函数关系式，并注明自变量x的取值范围；
（2）x为何值时，y有最大值？最大值是多少？

如图，已知抛物线y=﹣ax²+2ax+3a（a≠0）与x轴交于A、B两点，与y轴交于点C．

（1）请直接写出A、B两点的坐标．
（2）当a=，设直线AC与抛物线的对称轴交于点P，请求出△ABP的面积．

抛物线y=+x+m的顶点在直线y=x+3上，过点F（﹣2，2）的直线交该抛物线于点M、N两点（点M在点N的左边），MA⊥x轴于点A，NB⊥x轴于点B．

（1）先通过配方求抛物线的顶点坐标（坐标可用含m的代数式表示），再求m的值；
（2）设点N的横坐标为a，试用含a的代数式表示点N的纵坐标，并说明NF=NB；
（3）若射线NM交x轴于点P，且PA•PB=，求点M的坐标．

如图，抛物线y=﹣x²+2x+3与x轴相交于A、B两点（点A在点B的左侧），与y轴相交于点C，顶点为D．

（1）直接写出A、B、C三点的坐标和抛物线的对称轴；
（2）连接BC，与抛物线的对称轴交于点E，点P为线段BC上的一个动点，过点P作PF∥DE交抛物线于点F，设点P的横坐标为m；
①用含m的代数式表示线段PF的长，并求出当m为何值时，四边形PEDF为平行四边形？
②设△BCF的面积为S，求S与m的函数关系式．

如图，在平面直角坐标系xoy中，矩形ABCD的边AB在x轴上，且AB=3，BC=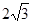，直线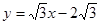经过点C，交y轴于点G．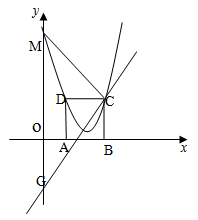

（1）求C,D坐标；
（2）已知抛物线顶点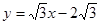上，且经过C，D,若抛物线与y交于点M连接MC,设点Q是线段下方此抛物线上一点，当点Q运动到什么位置时，△MCQ的面积最大？求出此时点Q的坐标和面积的最大值．
（3）将（2）中抛物线沿直线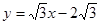平移，平移后的抛物线交y轴于点F，顶点为点E（顶点在y轴右侧）。平移后是否存在这样的抛物线，使⊿EFG为等腰三角形？若存在，请求 出此时抛物线的解析式；若不存在，请说明理由．

若一个三角形的三个顶点均在一个图形的不同的边上，则称此三角形为该图形的内接三角形．

（1）在图①中画出△ABC的一个内接直角三角形；
（2）如图②，已知△ABC中，∠BAC＝60°，∠B＝45°，AB＝8，AD为BC边上的高，探究以D为一个顶点作△ABC的内接三角形，其周长是否存在最小值？若存在，请求出最小值；若不存在，请说明理由；
（3）如图③，△ABC为等腰直角三角形，∠C＝90°，AC＝６，试探究：△ABC的内接等腰直角三角形的面积是否存在最小值？若存在，请求出最小值；若不存在，请说明理由．

如图，已知抛物线的顶点坐标为M（1,4），且经过点N（2,3），与x轴交于A、B两点（点A在点B左侧），与y轴交于点C。

（1）点A、B、C的坐标分别为        、        、        。
（2）若直线y=kx+t经过C、M两点，且与x轴交于点D，试证明四边形CDAN是平行四边形；
（3）点P在抛物线的对称轴x=1上运动，请探索：在x轴上方是否存在这样的P点，使以P为圆心的圆经过A、B两点，并且与直线CD相切，若存在，请求出点P的坐标；若不存在，请说明理由。

如图，在平面直角坐标系中，点的坐标分别为．

（1）请在图中画出，使得与关于点成中心对称；
（2）若一个二次函数的图象经过（1）中的三个顶点，求此二次函数的关系式．