初中数学二次函数在给定区间上的最值解答题

百货商店服装柜在销售中发现：某品牌童装平均每天可售出20件，每件盈利40元．为了迎接“六一”国际儿童节，商场决定采取适当的降价措施，扩大销售量，增加盈利，减少库存．经市场调查发现：如果每件童装降价1元，那么平均每天就可多售出2件．要想平均每天销售这种童装盈利1200元，那么每件童装应降价多少元？

如图，抛物线y=﹣x²+bx+c与x轴交于A（1，0），B（﹣3，0）两点．

（1）求该抛物线的解析式；
（2）设（1）中的抛物线交y轴与C点，在该抛物线的对称轴上是否存在点Q，使得△QAC的周长最小？若存在，求出Q点的坐标；若不存在，请说明理由；
（3）在（1）中的抛物线上的第二象限上是否存在一点P，使△PBC的面积最大？若存在，求出点P的坐标及△PBC的面积最大值；若没有，请说明理由．

某商场将进价为2000元的冰箱以2400元售出，平均每天能售出8台，为了配合国家“家电下乡”政策的实施，商场决定采取适当的降价措施．调查表明：这种冰箱的售价每降低50元，平均每天就能多售出4台．
（1）假设每台冰箱降价x元，商场每天销售这种冰箱的利润是y元，请写出y与x之间的函数表达式；（不要求写自变量的取值范围）
（2）商场要想在这种冰箱销售中每天盈利4800元，同时又要使百姓得到实惠，每台冰箱应降价多少元？
（3）每台冰箱降价多少元时，商场每天销售这种冰箱的利润最高？最高利润是多少？

已知抛物线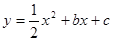的图像经过点O（0，0）A（6，0）。
（1）b =     ，c =     ；
（2）点B是x正半轴上的一动点，以OB为边在第一象限作一个正方形OBCD，使其一个顶点在抛物线上（不包括B点  ），画出示意图，求点B的坐标；
（3）在（2）的条件下，点E是线段BC上的一个动点，连结DE交线段AC与点F，则线段DF是否存在最小值，如果存在，请求出结果，如果不存在，请说明理由；

某玩具厂计划生产一种玩具熊猫，每日最高产量为40只，且每日产出的产品全部售出．已知生产x只玩具熊猫的成本为R（元），售价每只为P（元），且R、P与x的关系式分别为R＝500＋30x，P＝170－2x．
（1）当日产量为多少时，每日获得的利润为1750元？
（2）当日产量为多少时，可获得最大利润？最大利润是多少？

已知：抛物线经过点P（﹣1，﹣2b）（b、c为常量）．
（1）求b+c的值；
（2）证明：无论b、c取何值，抛物线与x轴都有两个交点．

浠水某商场要经营一种新上市的文具，进价为20元/件．试营销阶段发现：当销售单价是25元时，每天的销售量为250件；销售单价每上涨1元，每天的销售量就减少10件．
（1）写出商场销售这种文具，每天所得的销售利润w（元）与销售单价x（元）之间的函数关系式；
（2）求销售单价为多少元时，该文具每天的销售利润最大；
（3）商场的营销部结合上述情况，提出了A、B两种营销方案：
方案A：该文具的销售单价高于进价且不超过30元；
方案B：每天销售量不少于10件，且每件文具的利润至少为25元
请比较哪种方案的最大利润更高，并说明理由．

已知，如图，抛物线＞0）与轴交于点C，与轴交于A，B两点，点A在点B左侧．点B的坐标为（1，0），OC＝3OB．

（1）求抛物线的解析式；
（2）若点D是线段AC下方抛物线上的动点，求四边形ABCD面积的最大值；
（3）若点E在轴上，点P在抛物线上．是否存在以A，C，E，P为顶点且以AC为一边的平行四边形？若存在，直接写出点P的坐标；若不存在，请说明理由．

小明在课外学习时遇到这样一个问题：
定义：如果二次函数与满足，，，则称这两个函数互为“旋转函数”．
求函数的“旋转函数”．
小明是这样思考的：由函数可知，，，，根据，，，求出，，，就能确定这个函数的“旋转函数”．
请参考小明的方法解决下面问题：
（1）直接写出函数的“旋转函数”；
（2）若函数与互为“旋转函数”，求的值；
（3）已知函数的图象与轴交于点A、B两点（A在B的左边），与轴交于点C，点A、B、C关于原点的对称点分别是A₁，B₁，C₁，试证明经过点A₁，B₁，C₁的二次函数与函数互为“旋转函数”。

在“母亲节”期间，某校部分团员参加社会公益活动，准备购进一批许愿瓶进行销售，并将所得利润捐助给慈善机构．根据市场调查，这种许愿瓶一段时间内的销售量 （单位：个）与销售单价 （单位：元/个）之间的对应关系如图所示：

（1）与之间的函数关系是                     ．
（2）若许愿瓶的进价为6元/个，按照上述市场调查的销售规律，求销售利润 （单位：元）与销售单价 （单位：元/个）之间的函数关系式；
（3）若许愿瓶的进货成本不超过900元，要想获得最大利润，试确定这种许愿瓶的销售单价，并求出此时的最大利润．

如图，已知二次函数图象的顶点坐标为C（1,0），直线与该二次函数的图象交于A、B两点，其中A点的坐标为（3,4），B点在轴上．

（1）求的值及这个二次函数的关系式；
（2）P为线段AB上的一个动点（点P与A、B不重合），过P作轴的垂线与这个二次函数的图象交于点E点，设线段PE的长为，点P的横坐标为，求与之间的函数关系式，并写出自变量的取值范围；
（3）D为直线AB与这个二次函数图象对称轴的交点，在线段AB上是否存在一点P，使得四边形DCEP是平行四边形？若存在，请求出此时P点的坐标；若不存在，请说明理由．

某工厂生产的某种产品按质量分为1 0个档次．第1档次（最低档次）的产品一天能生产7 6件，每件利润10元．每提高一个档次，每件利润增加2元，但一天产量减少4件．若生产第x档次的产品一天的总利润为1080元，求该产品的质量档次．

如图，直线y=x+2与抛物线y=ax²+bx+6（a≠0）相交于A（，）和B（4，m），点P是线段AB上异于A、B的动点，过点P作PC⊥x轴于点D，交抛物线于点C．

（1）求抛物线的解析式；
（2）是否存在这样的P点，使线段PC的长有最大值？若存在，求出这个最大值；若不存在，请说明理由；
（3）求△PAC为直角三角形时点P的坐标．

一个批发商销售成本为20元/千克的某产品，根据物价部门规定：该产品每千克售价不得超过90元，在销售过程中发现的售量y（千克）与售价x（元/千克）满足一次函数关系，对应关系如下表：

售价x（元/千克）	…	50	60	70	80	…
销售量y（千克）	…	100	90	80	70	…

 
（1）求y与x的函数关系式；
（2）该批发商若想获得4000元的利润，应将售价定为多少元？
（3）该产品每千克售价为多少元时，批发商获得的利润w（元）最大？此时的最大利润为多少元？

二次函数y＝（m－2）x²＋（m＋3）x＋m＋2的图象过点（0，5）
（1）求m的值，并写出二次函数的表达式；
（2）求出二次函数图象的顶点坐标、对称轴。