初中数学二次函数在给定区间上的最值解答题

(本题14分)如图，在平面直角坐标系中．四边形OABC是平行四边形．直线经过O、C两点．点A的坐标为(8，o)，点B的坐标为(11．4)，动点P在线段OA上从点O出发以每秒1个单位的速度向点A运动，同时动点Q从点A出发以每秒2个单位的速度沿A→B→C的方向向点C运动，过点P作PM垂直于x轴，与折线O一C—B相交于点M。当P、Q两点中有一点到达终点时，另一点也随之停止运动，设点P、Q运动的时间为t秒()．△MPQ的面积为S．
（1）点C的坐标为___________，直线的解析式为___________．(每空l分，共2分)
（2）试求点Q与点M相遇前S与t的函数关系式，并写出相应的t的取值范围。
（3）试求题(2)中当t为何值时，S的值最大，并求出S的最大值。
（4）随着P、Q两点的运动，当点M在线段CB上运动时，设PM的延长线与直线相交于点N。试探究：当t为何值时，△QMN为等腰三角形？请直接写出t的值．

如图，抛物线与y轴交于A点，过点A的直线与抛物线交于另一点B，过点B作BC⊥x轴，垂足为点C(3，0).
（1）求直线AB的函数关系式；
（2）动点P在线段OC上从原点出发以每秒一个单位的速度向C移动，过点P作PN⊥x轴，交直线AB于点M，交抛物线于点N. 设点P移动的时间为t秒，MN的长度为s个单位，求s与t的函数关系式，并写出t的取值范围；
（3）设在（2）的条件下（不考虑点P与点O，点C重合的情况），连接CM，BN，当t为何值时，四边形BCMN为平行四边形？问对于所求的t值，平行四边形BCMN是否菱形？请说明理由.

已知抛物线与x轴没有交点．
（1）求c的取值范围；
（2）试确定直线经过的象限，并说明理由．

某商场销售一种进价为20元／台的台灯，经调查发现，该台灯每天的销售量w(太)与销售单价x(元)满足，设销售这种台灯每天的利润为y（元）。
（1）求y与x之间的函数关系式；
（2）当销售单价定为多少元时．每天的利润最大？最大利润是多少？
（3）在保证销售量尽可能大的前提下．该商场每天还想获得150元的利润．应将销售单价定为多少元？

如图，平面直角坐标系中，抛物线 $y=\frac{1}{2}{x}^2-2x=3$交 $y$轴于点 $A$， $P$为抛物线
上一点，且与点 $A$不重合．连结 $AP$，以 $AO$， $AP$为邻边作 $▱OAPQ$， $PQ$所在直线与 $x$轴交
于点 $B$．设点P的横坐标为 $m$．
（1）点 $Q$落在 $x$轴上时 $m$的值．
（3）若点 $Q$在 $x$轴下方，则 $m$为何值时，线段 $BQ$的长取最大值，并求出这个最大值．[参考公式：二次函数 $y=a{x}^2+bx+c\left(a\ne 0\right)$的顶点坐标为 $\left(-\frac{b}{2a}，\frac{4ac-b^2}{4a}\right)$]

已知二次函数 $y=-\frac{1}{2}{x}^2-x+\frac{3}{2}$

（1）在给定的直角坐标系中，画出这个函数的图象；
（2）根据图象，写出当 $y<0$时， $x$的取值范围；
（3）若将此图象沿 $x$轴向右平移3个单位，请写出平移后图象所对应的函数关系式．

已知抛物线的顶点是C (0，a) (a>0，a为常数)，并经过点(2a，2a)，点D（0，2a）为一定点.
(1)求含有常数a的抛物线的解析式；
(2)设点P是抛物线任意一点，过P作PH⊥x轴，垂足是H，求证：PD = PH；
(3)设过原点O的直线l与抛物线在第一象限相交于A、B两点，若DA=2DB，且S_△ABD = 4，求a的值.

 

（11·珠海）如图，Rt△OAB中，∠OAB＝90°，O为坐标原点，
边OA在x轴上，OA＝AB＝1个单位长度．把Rt△OAB沿x轴正方向平移1个单位长度后
得△AA₁B．
（1）求以A为顶点，且经过点B₁的抛物线的解析式；
（2）若（1）中的抛物线与OB交于点C，与y轴交于点D，求点D、C的坐标．

如图，在Rt△ABC中，∠C=90°，AC=8，BC=6，点P在AB上，AP=2，点E、F同时从点P出发，分别沿PA、PB以每秒1个单位长度的速度向点A、B匀速运动，点E到达点A后立刻以原速度沿AB向点B运动，点F运动到点B时停止，点E也随之停止．在点E、F运动过程中，以EF为边作正方形EFGH，使它与△ABC在线段AB的同侧．设E、F运动的时间为t/秒（t＞0），正方形EFGH与△ABC重叠部分面积为S．
（1）当时t=1时，正方形EFGH的边长是_______．当t=3时，正方形EFGH的边长是_______
（2）当0＜t≤2时，求S与t的函数关系式；
（3）直接答出：在整个运动过程中，当t为何值时，S最大？最大面积是多少？

如图．已知二次函数y=﹣x²+bx+3的图象与x轴的一个交点为A（4，0），与y轴交于点B．
（1）求此二次函数关系式和点B的坐标；
（2）在x轴的正半轴上是否存在点P．使得△PAB是以AB为底边的等腰三角形？若存在，求出点P的坐标；若不存在，请说明理由．

某农机服务站销售一批柴油，平均每天可售出20桶，每桶盈利40元．为了支援我市抗旱救灾，农机服务站决定采取降价措施．经市场调研发现：如果每桶柴油降价1元，农机服务站平均每天可多售出2桶．
（1）假设每桶柴油降价元，每天销售这种柴油所获利润为元，求与之间的函数关系式；
（2）每桶柴油降价多少元后出售，农机服务站每天销售这种柴油可获得最大利润？此时，与降价前比较，每天销售这种柴油可多获利多少元？

(本小题满分14分)平面直角坐标系中，平行四边形ABOC如图放置，点A、C的坐标分别为(0，3)、(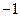，0)，将此平行四边形绕点0顺时针旋转90°，得到平行四边形。
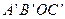(1)若抛物线过点C，A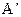，，求此抛物线的解析式；
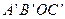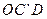(2)求平行四边形ABOC和平行四边形重叠部分△的周长；
(3)点M是第一象限内抛物线上的一动点，间：点M在何处时△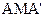的面积最大?最大面积是多少?并求出此时点M的坐标。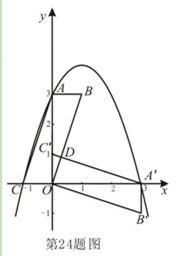

已知抛物线经过A(3，0), B(4，1)两点，且与y轴交于点C．
（1）求抛物线的函数关系式及点C的坐标；
（2）如图（1）,连接AB，在题（1）中的抛物线上是否存在点P，使△PAB是以AB为直角边的直角三角形？若存在，求出点P的坐标；若不存在，请说明理由；
（3）如图（2）,连接AC，E为线段AC上任意一点（不与A、C重合）经过A、E、O三点的圆交直线AB于点F，当△OEF的面积取得最小值时，求点E的坐标．

如图，抛物线与轴交于（，0）、（，0）两点，且，与轴交于点，其中是方程的两个根。
（1）求抛物线的解析式；
（2）点是线段上的一个动点，过点作∥，交于点，连接，当的面积最大时，求点的坐标；
（3）点在（1）中抛物线上，点为抛物线上一动点，在轴上是否存在点，使以为顶点的四边形是平行四边形，如果存在，求出所有满足条件的点的坐标，若不存在，请说明理由。

某商店以6元/千克的价格购进某种干果1140千克，并对其进行筛选分成甲级干果与乙级干果后同时开始销售．这批干果销售结束后，店主从销售统计中发出：甲级干果与乙级干果在销售过程中每天都有销量，且在同一天卖完；甲级干果从开始销售至销售的第x天的总销量y₁（千克）与x的关系为y₁=﹣x²+40x；乙级干果从开始销售至销售的第t天的总销量y₂（千克）与t的关系为y₂=at²+bt，且乙级干果的前三天的销售量的情况见下表：

t	1	2	3
y2	21	44	69

（1）求a、b的值；
（2）若甲级干果与乙级干果分别以8元/千克的6元/千克的零售价出售，则卖完这批干果获得的毛利润是多少元？
（3）问从第几天起乙级干果每天的销量比甲级干果每天的销量至少多6千克？
（说明：毛利润=销售总金额﹣进货总金额．这批干果进货至卖完的过程中的损耗忽略不计）