2011年初中毕业升学考试(贵州遵义卷)数学
我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例。如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出了 (n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律。例如,在三角形中第三行的三个数1,2,1,恰好对应
(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律。例如,在三角形中第三行的三个数1,2,1,恰好对应 展开式中的系数;第四行的四个数1,3,3,1,恰好对应着
展开式中的系数;第四行的四个数1,3,3,1,恰好对应着 展开式中的系数等等。
展开式中的系数等等。
(1)根据上面的规律,写出 的展开式。
的展开式。
(2)利用上面的规律计算:
6张不透明的卡片,除正面画有不同的图形外,其它均相同,把这6张卡片洗匀后,正面向下放在桌上,另外还有与卡片上图形形状完全相同的地板砖若干块,所有地板砖的长都相等。

⑴从这6张卡片中随机抽取一张,与卡片上图形形状相对应的这种地板砖能进行平面镶嵌的概率是多少?
⑵从这6张卡片中随机抽取2张,利用列表或画树状图计算:与卡片上图形形状相对应的这两种地板砖能进行平面镶嵌的概率是多少?
.在一次课题设计活动中,小明对修建一座87m长的水库大坝提出了以下方案;大坝的横截面为等腰梯形,如图, ∥
∥ ,坝高10m,迎水坡面
,坝高10m,迎水坡面 的坡度
的坡度 ,老师看后,从力学的角度对此方案提出了建议,小明决定在原方案的基础上,将迎水坡面
,老师看后,从力学的角度对此方案提出了建议,小明决定在原方案的基础上,将迎水坡面 的坡度进行修改,修改后的迎水坡面
的坡度进行修改,修改后的迎水坡面 的坡度
的坡度 。
。
(1) 求原方案中此大坝迎水坡 的长(结果保留根号)
的长(结果保留根号)
(2) 如果方案修改前后,修建大坝所需土石方总体积不变,在方案修改后,若坝顶沿 方向拓宽2.7m,求坝顶将会沿
方向拓宽2.7m,求坝顶将会沿 方向加宽多少米?
方向加宽多少米?
我州鼓苦荞茶、青花椒、野生蘑菇,为了让这些珍宝走出大山,走向世界,州政府决定组织21辆汽车装运这三种土特产共120吨,参加全国农产品博览会。现有A型、B型、C型三种汽车可供选择。已知每种型号汽车可同时装运2种土特产,且每辆车必须装满。根据下表信息,解答问题。
| |
 |
苦荞茶 |
青花椒 |
野生蘑菇 |
|
| 每 辆 汽 车 运 载 量 |
(吨) |
A型 |
 2 2 |
2 |
|
| B型 |
4 |
|
2 |
||
| C型 |
|
1 |
6 |
| 车型 |
A |
B |
C |
| 每辆车运费(元) |
1500 |
1800 |
2000 |
(1) 设A型汽车安排 辆,B 型汽车安排
辆,B 型汽车安排 辆,求
辆,求 与
与 之间的函数关系式。
之间的函数关系式。
(2) 如果三种型号的汽车都不少于4辆,车辆安排有几种方案?并写出每种方案。
(3) 为节约运费,应采用(2)中哪种方案?并求出最少运费。
如图,抛物线与 轴交于
轴交于 (
( ,0)、
,0)、 (
( ,0)两点,且
,0)两点,且 ,与
,与 轴交于点
轴交于点 ,其中
,其中 是方程
是方程 的两个根。
的两个根。
(1)求抛物线的解析式;
(2)点 是线段
是线段 上的一个动点,过点
上的一个动点,过点 作
作 ∥
∥ ,交
,交 于点
于点 ,连接
,连接 ,当
,当 的面积最大时,求点
的面积最大时,求点 的坐标;
的坐标;
(3)点 在(1)中抛物线上,点
在(1)中抛物线上,点 为抛物线上一动点,在
为抛物线上一动点,在 轴上是否存在点
轴上是否存在点 ,使以
,使以 为顶点的四边形是平行四边形,如果存在,求出所有满足条件的点
为顶点的四边形是平行四边形,如果存在,求出所有满足条件的点 的坐标,若不存在,请说明理由。
的坐标,若不存在,请说明理由。
某地区有8所高中和22所初中.要了解该地区中学生的视力情况,下列抽样方式获得的数据最能反映该地区中学生视力情况的是( )
| A.从该地区随机选取一所中学里的学生 | B.从该地区30所中学里随机选取800名学生 |
| C.从该地区一所高中和一所初中各选取一个年级的学生 | D.从该地区的22所初中里随机选取400名学生 |
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.若AC= ,BC=2,则sin∠ACD的值为( )
,BC=2,则sin∠ACD的值为( )
A、 B、
B、
C、 D、
D、
某种生物细胞的直径约为0.00056 ,将0.00056用科学记数法表示为
,将0.00056用科学记数法表示为
A.0.56 |
B. 5.6 |
C.5.6 |
D.56 |
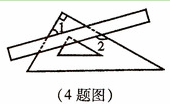
.把一块直尺与一块三角板如图放置,若 o,则
o,则 的度数为
的度数为
| A.115o | B.120o |
| C.145o | D.135o |
今年5月,某校举行“唱红歌”歌咏比赛,有17位同学参加选拔赛,所得分数互
不相同,按成绩取前8名进入决赛,若知道某同学分数,要判断他能否进入决赛,只需知道
17位同学分数的
| A.中位数 | B.众数 | C.平均数 | D.方差 |
如图, 是⊙
是⊙ 的直径,
的直径, 交⊙
交⊙ 于点
于点 ,
, ⊥
⊥ 于点
于点 ,要使
,要使
是⊙的切线,还需补充一个条件,则补充的条件不正确的是
A. |
B. |
C. |
D. ∥ ∥ |

如图,在直角三角形 中(∠
中(∠ =90o),放置边长分别3,4,
=90o),放置边长分别3,4, 的三个正方形,
的三个正方形,
则 的值为
的值为
| A.5 | B.6 |
| C.7 | D.12 |

如图,由四个边长为1的小正方形构成一个大正方形,连接小正方形的三个顶点,
可得到△ ,则△
,则△ 中
中 边上的高是 ▲ .
边上的高是 ▲ .
有一数值转换器,原理如图所示,若开始输入 的值是5,可发现第一次输出的结果是8,第二次输出的结果是4,……,请你探索第2011次输出的结果是 ▲ .
的值是5,可发现第一次输出的结果是8,第二次输出的结果是4,……,请你探索第2011次输出的结果是 ▲ .
如图,已知双曲线 ,
, ,点P为双曲线
,点P为双曲线 上的
上的
一点,且PA⊥ 轴于点A,PB⊥
轴于点A,PB⊥ 轴于点B,PA、PB分别交双曲线
轴于点B,PA、PB分别交双曲线 于D、C两点,则
于D、C两点,则
△PCD的面积为 ▲ .
(8分)某市为缓解城市交通压力,决定修建人行天桥,原设计天桥的楼梯长AB=6 ,∠ABC=45o,后考虑到安全因素,将楼梯脚B移到CB延长线上点D处,使
,∠ABC=45o,后考虑到安全因素,将楼梯脚B移到CB延长线上点D处,使 (如图所示).
(如图所示).
(1)求调整后楼梯AD的长;
(2)求BD的长.
(结果保留根号)
(10分))第六次全国人口普查工作圆满结束,2011年5月20日《遵义晚报》报到了遵义市人口普查结果,并根据我市常住人口情况,绘制出不同年龄段的扇形统计图;普查结果显示,2010年我市常住人口中,每10万人就有4402人具有大学文化程度,与2000年第五次人口普查相比,是2000年每10万人具有大学文化程度人数的3倍少473人,请根据以上信息,解答下列问题.
(1)65岁及以上人口占全市常住人口的百分比是 ▲ ;
(2)我市2010年常住人口约为 ▲ 万人(结果保留四个有效数字);
(3)与2000年我市常住人口654.4万人相比,10年间我市常住人口减少 ▲ 万人;
(4)2010年我市每10万人口中具有大学文化程度人数比2000年增加了多少人?
(10分) 把一张矩形ABCD纸片按如图方式折叠,使点A与点E重合,点C与点F重合(E、F两点均在BD上),折痕分别为BH、DG.
(1)求证:△BHE≌△DGF;
(2)若AB=6cm,BC=8cm,求线段FG的长.
有四张卡片(背面完全相同),分别写有数字1、2、-1、-2,把它们背面朝
上洗匀后,甲同学抽取一张记下这个数字后放回洗匀,乙同学再从中抽出一张,记下这个
数字,用字母b、c分别表示甲、乙两同学抽出的数字.
(1)用列表法求关于 的方程
的方程 有实数解的概率;
有实数解的概率;
(2)求(1)中方程有两个相等实数解的概率.
“六·一”儿童节前,某玩具商店根据市场调查,用2500元购进一批儿童玩
具,上市后很快脱销,接着又用4500元购进第二批这种玩具,所购数量是第一批数量的1.5
倍,但每套进价多了10元.
(1)求第一批玩具每套的进价是多少元?
(2)如果这两批玩具每套售价相同,且全部售完后总利润不低于25%,那么每套售价至少是多少元?
如图,梯形ABCD中,AD∥BC,BC=20cm,AD=10cm,现有两个动点P、Q
分别从B、D两点同时出发,点P以每秒2cm的速度沿BC向终点C移动,点Q以每秒1cm
的速度沿DA向终点A移动,线段PQ与BD相交于点E,过E作EF∥BC交CD于点F,射线
QF交BC的延长线于点H,设动点P、Q移动的时间为t(单位:秒,0<t<10).
(1)当t为何值时,四边形PCDQ为平行四边形?
(2)在P、Q移动的过程中,线段PH的长是否发生改变?如果不变,求出线段PH的长;如果改变,请说明理由.
 中,
中, ,
, ,点
,点 为
为 的中点,
的中点,
 ,垂足为点
,垂足为点 ,则
,则




 ,点C在
,点C在 上,且点C不与A、B重合,则
上,且点C不与A、B重合,则 的度数为( )
的度数为( )
 B.
B. 或
或 D.
D. 的解为( )
的解为( )








 的图像如图所示,反比列函数
的图像如图所示,反比列函数 与正比列函数
与正比列函数 在同一坐标系内的大致图像是( )
在同一坐标系内的大致图像是( )
 。
。 ”的逆命题改写成“如果……,那么……”的形式:
”的逆命题改写成“如果……,那么……”的形式: 
 的值是 。
的值是 。
 是平行四边形
是平行四边形 的对角线
的对角线 上的点,
上的点, ,请你猜想:线段
,请你猜想:线段 与线段
与线段 有怎样的关系?并对你的猜想加以证明。
有怎样的关系?并对你的猜想加以证明。
 三个顶点的坐标分别为
三个顶点的坐标分别为

 所在直线的解析式。
所在直线的解析式。 顺时针旋转
顺时针旋转 后得到的
后得到的 ,并求出
,并求出 为有理数,
为有理数, 分别表示
分别表示 的整数部分和小数部分,且
的整数部分和小数部分,且
 ,则
,则 。
。 ,高为
,高为 ,点
,点 分别是圆柱两底面圆周上的点,且
分别是圆柱两底面圆周上的点,且 、
、 在同一母线上,用一棉线从
在同一母线上,用一棉线从 。
。 ,以
,以 为直径,
为直径, 为圆心的半圆交
为圆心的半圆交 于点
于点 ,点
,点 为
为
 的中点,连接
的中点,连接 交
交 ,
, 为
为 的角平分线,且
的角平分线,且 ,垂足为点
,垂足为点 。
。
 是半圆
是半圆 ,
, ,求
,求


 在实数范围内有意义,则x的取值范围( )
在实数范围内有意义,则x的取值范围( )





 的函数值
的函数值 随
随 的增大而减小,则
的增大而减小,则 的取值范围是
的取值范围是



 、
、 均为正整数,且
均为正整数,且 ,则
,则 的最小值是
的最小值是 = ▲ .
= ▲ . 的解为 ▲ .
的解为 ▲ . 、
、 为实数,且
为实数,且 ,则
,则 = ▲ .
= ▲ . 是边长为2的等边△
是边长为2的等边△ 的内切圆,则⊙
的内切圆,则⊙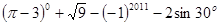
 ,其中
,其中 .
. 经过A(3,0), B(4,1)两点,且与y轴交于点C.
经过A(3,0), B(4,1)两点,且与y轴交于点C.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号