初中数学二次函数在给定区间上的最值解答题

（本小题满分6分）
已知：二次函数y=x²+bx+c，其图象对称轴为直线x=1，且经过点（2，–）.
（1）求此二次函数的解析式.
（2）设该图象与x轴交于B、C两点（B点在C点的左侧），请在此二次函数x轴下方的图
象上确定一点E，使△EBC的面积最大，并求出最大面积.
注：二次函数y=x²+bx+c（≠0）的对称轴是直线x=－.

如图，在平面直角坐标系中，直线与抛物线交于A、B两点，点A在x轴上，点B的横坐标为－8.
（1）求该抛物线的解析式；
（2）点P是直线AB上方的抛物线上一动点（不与点A、B重合），过点P作x轴的垂线，垂足为C，交直线AB于点D，作PE⊥AB于点E.
①设△PDE的周长为l，点P的横坐标为x，求l关于x的函数关系式，并求出l的最大值；
②连接PA，以PA为边作图示一侧的正方形APFG.随着点P的运动，正方形的大小、位置也随之改变.当顶点F或G恰好落在y轴上时，直接写出对应的点P的坐标.
    

如图，y关于x的二次函数y=﹣（x+m）（x﹣3m）图象的顶点为M，图象交x轴于A、B两点，交y轴正半轴于D点．以AB为直径作圆，圆心为C．定点E的坐标为（﹣3，0），连接ED．（m＞0）
（1）写出A、B、D三点的坐标；
（2）当m为何值时M点在直线ED上？判定此时直线与圆的位置关系；
（3）当m变化时，用m表示△AED的面积S，并在给出的直角坐标系中画出S关于m的函数图象的示意图．

2010年上半年，某种农产品受不良炒作的影响，价格一路上扬．8月初国家实施调控措施后，该农产品的价格开始回落．其中，1月份至7月份，该农产品的月平均价格y元/千克与月份x呈一次函数关系；7月份至12月份，月平均价袼y元/千克与月份x呈二次函数关系．已知1月、7月、9月和12月这四个月的月平均价格分别为8元/千克、26元/千克、14元/千克、11元/千克．
（1）分别求出当1≤x≤7和7≤x≤12时，y关于x的函数关系式；
（2）2010年的12个月中．这种农产品的月平均价格哪个月最低？最低为多少？
（3）若以12个月份的月平均价格的平均数为年平均价格，月平均价格高于年平均价格的月份有哪些？

如图，已知抛物线经过A（﹣2，0），B（﹣3，3）及原点O，顶点为C．
（1）求抛物线的解析式；
（2）若点D在抛物线上，点E在抛物线的对称轴上，且A、O、D、E为顶点的四边形是平行四边形，求点D的坐标；
（3）P是抛物线上的第一象限内的动点，过点P作PMx轴，垂足为M，是否存在点P，使得以P、M、A为顶点的三角形△BOC相似？若存在，求出点P的坐标；若不存在，请说明理由．

如图，抛物线y=x²+bx+c的顶点为D（﹣1，﹣4），与y轴交于点C（0，﹣3），与x轴交于A，B两点（点A在点B的左侧）．
（1）求抛物线的解析式；
（2）连接AC，CD，AD，试证明△ACD为直角三角形；
（3）若点E在抛物线的对称轴上，抛物线上是否存在点F，使以A，B，E，F为顶点的的四边形为平行四边形？若存在，求出所有满足条件的点F的坐标；若不存在，请说明理由．

在平面直角坐标系xOy中，二次函数y=mx²+（m﹣3）x﹣3（m＞0）的图象与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C．
（1）求点A的坐标；
（2）当∠ABC=45°时，求m的值；
（3）已知一次函数y=kx+b，点P（n，0）是x轴上的一个动点，在（2）的条件下，过点P垂直于x轴的直线交这个一次函数的图象于点M，交二次函数y=mx²+（m﹣3）x﹣3（m＞0）的图象于N．若只有当﹣2＜n＜2时，点M位于点N的上方，求这个一次函数的解析式．

【问题情境】已知矩形的面积为a（a为常数，a＞0），当该矩形的长为多少时，它的周长最小？最小值是多少？
【数学模型】

设该矩形的长为x，周长为y，则y与x的函数关系式为y=2（x+）（x＞0）．
【探索研究】（1）我们可以借鉴以前研究函数的经验，先探索函数y=x+（x＞0）的图象和性质．
①填写下表，画出函数的图象；

x	…				1	2	3	4	…
y	…								…

②观察图象，写出该函数两条不同类型的性质；
③在求二次函数y=ax²+bx+c（a≠0）的最大（小）值时，除了通过观察图象，还可以通过配方得到．请你通过配方求函数y=x+（x＞0）的最小值
【解决问题】
（2）用上述方法解决“问题情境”中的问题，直接写出答案．

已知函数y=mx²﹣6x+1（m是常数）．
（1）求证：不论m为何值，该函数的图象都经过y轴上的一个定点；
（2）若该函数的图象与x轴只有一个交点，求m的值．

如图，在直角坐标系中，梯形ABCD的底边AB在x轴上，底边CD的端点D在y轴上.直线CB的表达式为y=－x+，点A、D的坐标分别为（－4，0），（0，4）.动点P自A点出发，在AB上匀速运行.动点Q自点B出发，在折线BCD上匀速运行，速度均为每秒1个单位.当其中一个动点到达终点时，它们同时停止运动.设点P运动t（秒）时，△OPQ的面积为s（不能构成△OPQ的动点除外）.
（1）求出点B、C的坐标；
（2）求s随t变化的函数关系式；
（3）当t为何值时s有最大值？并求出最大值.

如图所示，过点F（0，1）的直线y=kx＋b与抛物线交于M（x₁，
y₁）和N（x₂，y₂）两点（其中x₁＜0，x₂＜0）．
⑴求b的值．
⑵求x₁•x₂的值
⑶分别过M、N作直线l：y=－1的垂线，垂足分别是M₁、N₁，判断△M₁FN₁的形状，并证明你的结论．
⑷对于过点F的任意直线MN，是否存在一条定直线m，使m与以MN为直径的圆相切．如果有，请法度出这条直线m的解析式；如果没有，请说明理由．

我市某镇的一种特产由于运输原因，长期只能在当地销售．当地政府对
该特产的销售投资收益为：每投入x万元，可获得利润（万元）．当
地政府拟在“十二•五”规划中加快开发该特产的销售，其规划方案为：在规划前后对该项
目每年最多可投入100万元的销售投资，在实施规划5年的前两年中，每年都从100万元中
拨出50万元用于修建一条公路，两年修成，通车前该特产只能在当地销售；公路通车后的
3年中，该特产既在本地销售，也在外地销售．在外地销售的投资收益为：每投入x万元，
可获利润（万元）
⑴若不进行开发，求5年所获利润的最大值是多少？
⑵若按规划实施，求5年所获利润（扣除修路后）的最大值是多少？
⑶根据⑴、⑵，该方案是否具有实施价值？

已知两直线l₁，l₂分别经过点A（1，0），点B（﹣3，0），并且当两直线同时相交于y正半轴的点C时，恰好有l₁⊥l₂，经过点A、B、C的抛物线的对称轴与直线l₂交于点K，如图所示．
（1）求点C的坐标，并求出抛物线的函数解析式；
（2）抛物线的对称轴被直线l₁，抛物线，直线l₂和x轴依次截得三条线段，问这三条线段有何数量关系？请说明理由；
（3）当直线l₂绕点C旋转时，与抛物线的另一个交点为M，请找出使△MCK为等腰三角形的点M，简述理由，并写出点M的坐标．

在平面直角坐标系中，如图1，将n个边长为1的正方形并排组成矩形OABC，相邻两边OA和OC分别落在x轴和y轴的正半轴上，设抛物线y=ax²+bx+c（a＜0）过矩形顶点B、C．
（1）当n=1时，如果a=﹣1，试求b的值；
（2）当n=2时，如图2，在矩形OABC上方作一边长为1的正方形EFMN，使EF在线段CB上，如果M，N两点也在抛物线上，求出此时抛物线的解析式；
（3）将矩形OABC绕点O顺时针旋转，使得点B落到x轴的正半轴上，如果该抛物线同时经过原点O．
①试求当n=3时a的值；
②直接写出a关于n的关系式．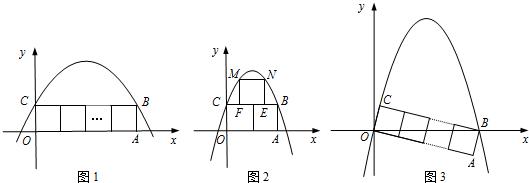

使得函数值为零的自变量的值称为函数的零点。例如，对于函数，令y=0，可得x=1，我们就说1是函数的零点。
己知函数 (m为常数)。
（1）当=0时，求该函数的零点；
（2）证明：无论取何值，该函数总有两个零点；
（3）设函数的两个零点分别为和，且，此时函数图象与x轴的交点分
别为A、B(点A在点B左侧)，点M在直线上，当MA+MB最小时，求直线AM的函数解析式。