二次函数y=ax2+c中,当x=3时,y="26" ;当x=2时,y="11" ;则当x=5时,
y= __ .
、分别说出下列二次函数的二次项系数、一次项系数和常数项:
(1)d=n2-n, (2)y=1-x2, (3)y=-x(x-3)
分别说出下列函数的名称:
(1)y=2x-1 (2)y=-3x2, (3)y= (4)y=3x-x2 (5)y=x
已知二次函数 的图象与
的图象与 轴交于点
轴交于点 (
( ,0)、点
,0)、点 ,与
,与 轴交于点
轴交于点 .
.
(1)求点 坐标;
坐标;
(2)点 从点
从点 出发以每秒1个单位的速度沿线段
出发以每秒1个单位的速度沿线段 向
向 点运动,到达点
点运动,到达点 后停止运动,过点
后停止运动,过点 作
作 交
交 于点
于点 ,将四边形
,将四边形 沿
沿 翻 折,得到四边形
翻 折,得到四边形 ,设点
,设点 的运动时间为
的运动时间为 .
.
①当 为何值时,点
为何值时,点 恰好落在二次函数
恰好落在二次函数 图象的对称轴上;
图象的对称轴上;
②设四边形 落在第一象限内的图形面积为
落在第一象限内的图形面积为 ,求
,求 关于
关于 的函数关系式,并求出
的函数关系式,并求出 的最大值.
的最大值.
已知抛物线 :
: 的顶点在坐标轴上.
的顶点在坐标轴上.
(1)求 的值;
的值;
(2) 时,抛物线
时,抛物线 向下平移
向下平移 个单位后与抛物线
个单位后与抛物线 :
: 关于
关于 轴对称,且
轴对称,且 过点
过点 ,求
,求 的函数关系式;
的函数关系式;
(3) 时,抛物线
时,抛物线 的顶点为
的顶点为 ,且过点
,且过点 .问在直线
.问在直线 上是否存在一点
上是否存在一点 使得△
使得△ 的周长最小,如果存在,求出点
的周长最小,如果存在,求出点 的坐标, 如果不存在,请说明理由.
的坐标, 如果不存在,请说明理由.
已知:如图,抛物线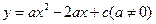 与
与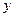 轴交于点
轴交于点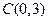 ,与
,与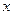 轴交于
轴交于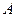 、
、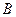 两点,点
两点,点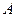 的坐标为
的坐标为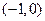 .
.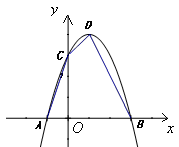
(1)求抛物线的解析式及顶点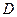 的坐标;
的坐标;
(2)设点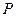 是在第一象限内抛物线上的一个动点,求使与四边形
是在第一象限内抛物线上的一个动点,求使与四边形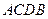 面积相等的四边形
面积相等的四边形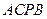 的点
的点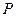 的坐标;
的坐标;
(3)求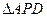 的面积.
的面积.
.已知平面直角坐标系xOy中, 抛物线 与直线
与直线 的一个公共点为
的一个公共点为 .
.
(1)求此抛物线和直线的解析式;
(2)若点P在线段OA上,过点P作y轴的平行线交(1)中抛物线于点Q,求线段PQ长度的最大值;
(3)记(1)中抛物线的顶点为M,点N在此抛物线上,若四边形AOMN恰好是梯形,求点N的坐标及梯形AOMN的面积.
已知关于 的方程
的方程 .
.
(1)求证:方程总有两个实数根;
(2)若方程有一个根大于4且小于8,求m的取值范围;
(3)设抛物线 与
与 轴交于点M,若抛物线与x轴的一个交点关于直线
轴交于点M,若抛物线与x轴的一个交点关于直线 的对称点恰好是点M,求
的对称点恰好是点M,求 的值.
的值.
(本小题满分8分)
如图,抛物线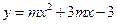 (
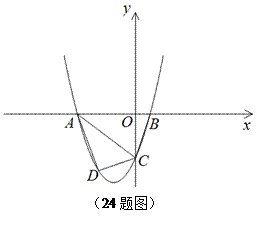
(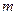 >0)与y轴交于点C,与x轴交于A 、B两点,点 A在点B的左侧,且
>0)与y轴交于点C,与x轴交于A 、B两点,点 A在点B的左侧,且 .
.
(1)求此抛物线的解析式;
(2)如果点D是线段AC下方抛物线上的动点,设D点的横坐标为x,
△ACD的面积为S,求S与x的关系式,并求当S最大时点D的坐标;
(3)若点E在x轴上,点P在抛物线上,是否存在以A、C、E、P为顶点的平行四边形?若存在求点P坐标;若不存在,请说明理由.
(本小题满分7分)
已知:关于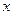 的一元二次方程
的一元二次方程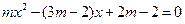 .
.
(1)若方程有两个不相等的实数根,求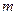 的取值范围;
的取值范围;
(2)在(1)的条件下,求证:无论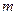 取何值,抛物线y=
取何值,抛物线y=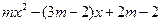 总过
总过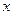 轴上的一个固定点;
轴上的一个固定点;
(3)若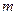 为正整数,且关于
为正整数,且关于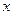 的一元二次方程
的一元二次方程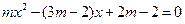 有两个不相等的整数根,把抛物线y=
有两个不相等的整数根,把抛物线y=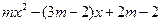 向右平移4个单位长度,求平移后的抛物线的解析式.
向右平移4个单位长度,求平移后的抛物线的解析式.
二次函数 的图象如图所示,根据图象解答下列问题:
的图象如图所示,根据图象解答下列问题:
(1)写出方程 的两个根;
的两个根;
(2)写出 随
随 的增大而减小的自变量
的增大而减小的自变量 的取值范围;
的取值范围;
如图有一座抛物线形拱桥,桥下面在正常水位是AB宽20m,水位上升3m就达到警戒线CD,这是水面宽度为10m。
(1)在如图的坐标系中求抛物线的解析式。
(2)若洪水到来时,水位以每小时0.2m的速度上升,从警戒线开始,再持续多少小时才能到拱桥顶?
2010年度东风公司神鹰汽车改装厂开发出A型农用车,其成本价为每辆2万元,出厂价为每辆2.4万元,年销售价为10000辆,2011年为了支援西部大开发的生态农业建设,该厂抓住机遇,发展企业,全面提高A型农用车的科技含量,每辆农用车的成本价增长率为x,出厂价增长率为0.75x,预测年销售增长率为0.6x.(年利润=(出厂价-成本价)×年销售量)
(1)求2011年度该厂销售A型农用车的年利润y(万元)与x之间的函数关系。
(2)该厂要是2001年度销售A型农用车的年利润达到4028万元,该年度A型农用车的年销售量应该是多少辆?
已知二次函数y=x2+bx+c的图像与x轴的两个交点的横坐标分别为x1、x2,一元二次方程x2+b2x+20=0的两实根为x3、x4,且x2-x3=x1-x4=3,求二次函数的解析式,并写出顶点坐标。
某商场将进价为30元的书包以40元售出,平均每月能售出600个,调查表明:这种书包的售价每上涨1元,其销售量就减少10个。
(1)请写出每月售出书包的利润y元与每个书包涨价x元间的函数关系式;
(2)设每月的利润为10000的利润是否为该月最大利润?如果是,请说明理由;如果不是,请求出最大利润,并指出此时书包的售价应定为多少元。
(3)请分析并回答售价在什么范围内商家就可获得利润。