初中数学二次函数在给定区间上的最值解答题

已知：o为坐标原点，∠ AOB=300  , ∠ABO=900 且A(2,0)求: 过A、B、O三点的二次函数解析式

已知如图，二次函数y="ax2" +bx+c的图像过A、B、C三点

观察图像写出A、B、C三点的坐标
求出二次函数的解析式

已知二次函的图象过点（0， 5）
⑴ 求m的值，并写出二次函数的关系式；
⑵ 求出二次函数图象的顶点坐标、对称轴．

已知二次函数y=-x2 –x+4回答下列问题
（1）用配方法将其化成y="a" (x-h)2+k的形式
（2）指出抛物线的顶点坐标和对称轴
（3）当x取何值时，y随x增大而增大;
当x取何值时，y随x增大而减小？

二次函数过A(-1,0) B(0,-3)两点，且对称轴是X=1求出它的解析式

某公司推出了一种高效环保型洗涤用品，年初上市后，公司经历了从亏损到盈利的过程，下面的二次函数的图象(部分)刻画了该公司年初以来累积利润S(万元)与销售时间t(月)之间的关系(即前t个月的利润总和S与t之间的关系).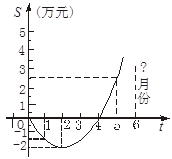

(1)根据图象你可获得哪些关于该公司的具体信息？(至少写出三条)
(2)还能提出其他相关的问题吗？若不能，说明理由；若能，进行解答，并与同伴交流.

如图，一位篮球运动员跳起投篮，球沿抛物线y＝－x2＋3.5运行，然后准确落入框内。已知篮框的中心离地面的距离为3.05米。求：

(1)球在空中运行的最大高度为多少米?
(2)如果该运动员跳投时，球出手离地面的高度为2.25米，请问他距离篮框中心的水平距离是多少?

已知二次函数，求证：它的图象与x轴总有两个交点。

抛物线y＝ax2＋bx＋c与直线y＝x－2相交于(m，－2)，(n，3)两点，且抛物线的对称轴为直线x＝3，求抛物线的解析式。

抛物线y＝x2＋x－k与直线y＝－2x＋1的交点的纵坐标为3。
(1)求抛物线的解析式
(2)求抛物线y＝x2＋x－k与直线y＝－2x＋1的另一个交点坐标．

利用函数的图象求下列方程的解：(1)x2＋x－6＝0；    (2)2x2－3x－5＝0

2010年8月31日，全国绿化委员会、 国家林业局、 重庆市人民政府共同发起“绿化长江重庆行动”， 该行动就是要加快长江两岸造林绿化步伐，保护母亲河，促进入与自然和谐共生．某园艺公司从 9 月开始积极响应这一行动，进行植树造林．该公司第 x 月种植树木的亩数 y(亩)与 x 之间满足，(其中x从9月算起，即9月时 x=l，10月时x=2，…，且，x为正整数)．但由于植树规模增加，每亩的收益会相应降低，每亩的收益 P(千元)与种植树木亩数 y(亩)之间的关系如下表：

亩数y(亩)	5	6	7	8	…
每亩收益P(千元／亩)	46	44	42	40	…

(1)请观察题中的表格，用所学过的一次函数、二次函数和反比例函数的有关知识求出 P与 y 之间所 满足的函数关系表达式：
(2)求该行动实施六个月来，第几月的总收益最大？此时每亩收益为多少？
(3)进入三月份，便是植树造林的“黄金期”，为此政府出台了一项激励措施：在“植树造林”过程中， 每月植树面积与二月份植树面积相同的部分，按二月份每亩收益进行结算；超出二月份植树面积 的部分，每亩收益将按二月份时每亩的收益再增加 0.6a%进行结算．这样，该公司三月份植树面积比二月份的植树面积增加了a%．另外，三月份时公司需对三月份之前种植的所有树木进行保养， 除去成本后政府给予每亩 5a%千元的保养补贴．最后，该公司三月份获得种植树木的收益和政府 保养补贴共 702 千元．请通过计算，估算出 a 的整数值．
(参考数据：)

[应用题]如图,一单杠高2.2米,两立柱之间的距离为1.6米,将一绳子的两端拴于立柱与铁杠结合处,绳子自然下垂呈抛物线状.

（1）如图(1)一身高为0.7米的小孩站在离立柱0.4米处,其头部刚好触到绳子,求绳子最低点到地面的距离;
(2)如图(2),为供孩子们打秋千,把绳子剪断后,中间系一块长为0.4米的木板.除掉系木板用去的绳子后,两边的绳子长正好各为2米,木板与地面平行.求这时木板离地面的距离(参考数据:≈1.8, ≈1.9, ≈2.1).

已知：某租赁公司出租同一型号的设备40套，当每套月租金为270元时，恰好全部租出。在此基础上，每套月租金每增加10元，就少租出1套设备。而未租出的设备每月需支付各种费用每套20元。
设每套设备实际月租金为x元（x≥270元），月收益为y元（总收益＝设备租金收入－未租出设备费用）
问题1： 求y与x的二次函数关系式
问题2： 当x为何值时，月收益最大？最大值是多少？
问题3： 当月租金分别为300元/每套和350元/每套时，月收益各是多少？根据月收益的计算结果，此时公司应该选择出租多少套设备更合适，请简要说明理

某宾馆有50个房客供游客居住,当每个房间的定价为每天180元时,房间会全部住满,当每个房间的定价每增加10元时,就会有一个房间空闲,如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用。房价定为多少时，宾馆利润最大？