河南省扶沟县初三下册26章《二次函数及其图像》检测题
如图,小明在楼上点A处观察旗杆BC,测得旗杆顶部B的仰角为30°,测得旗杆底部C的俯角为60°,已知点A距地面高AD为12m,求旗杆的高度。(12')
如图,A、B是两座现代化城市,C是一个古城遗址,C城在A城的北偏东30°方向,在B城的北偏西45°方向,且C城与A城相距120千米,B城在A城的正东方向,以C为圆心,以60千米为半径的圆形区域内有古迹和地下文物,现要在A、B两城市间修建一条笔直的高速公路,(14')
(1)请你计算公路的长度。(结果保留根号)
(2)请你分析这条公路有没有可能是对古迹或文物赞成损毁。
对于抛物线 ,下列说法正确的是( )
,下列说法正确的是( )
A.开口向下,顶点坐标 |
B.开口向上,顶点坐标 |
C.开口向下,顶点坐标 |
D.开口向上,顶点坐标 |
已知二次函数y=ax2+bx的图象经过点A(-1,1),则ab有 ( )
| A.最小值0; | B.最大值 1; | C.最大值2; | D.有最小值 |
若A( ),B(
),B( ),C(
),C( )为二次函数
)为二次函数 的图象上的三点,则
的图象上的三点,则

 的大小关系是( )
的大小关系是( )
A. |
B. |
C. |
D. |
二次函数y=kx2-6x+3的图象与 轴有两个交点,则
轴有两个交点,则 的取值范围是( )
的取值范围是( )
A. |
B. |
C.k≤3 | D.k≤3且k≠0 |
抛物线 向右平移1个单位,再向下平移2个单位,所得到的抛物线是( )
向右平移1个单位,再向下平移2个单位,所得到的抛物线是( )
(A) (B)
(B)
(C) (D)
(D)
烟花厂为扬州三月经贸旅游节特别设计制作一种新型礼炮,这种礼炮的升空高度 与飞行时间
与飞行时间 的关系式是
的关系式是 ,若这种礼炮在点火升空到最高点处引爆,则从点火升空到引爆需要的时间为( )
,若这种礼炮在点火升空到最高点处引爆,则从点火升空到引爆需要的时间为( )
A. |
B. |
C. |
D. |
把二次函数 的图象向左平移2个单位,再向上平移1个单位,所得到的图象对应的二次函数关系式是( )
的图象向左平移2个单位,再向上平移1个单位,所得到的图象对应的二次函数关系式是( )
A. ; ; |
B. ; ; |
C. |
D. |
(3)已知抛物线y=ax2+bx,当a>0,b<0时,它的图象经过( )
| A.一、二、三象限 ; | B.一、二、四象限; | C.一、三、四象限; | D.一、二、三、四象限. |
、若 ,则二次函数
,则二次函数 的图象的顶点在 ( )
的图象的顶点在 ( )
| A.第一象限; | B.第二象限; | C.第三象限; | D.第四象限 |
、不论x为何值,函数y=ax2+bx+c(a≠0)的值恒大于0的条件是( )
| A.a>0,△>0; | B.a>0, △<0; | C.a<0, △<0; | D.a<0, △<0 |
如图,已知点M(p,q)在抛物线y=x2-1上,以M为圆心的圆与x轴交于A、B两点,且A、B两点的横坐标是关于x的方程x2-2px+q=0的两根,则弦AB的长等于 。
已知二次函数y=ax2(a≥1)的图像上两点A、B的横坐标分别是-1、2,点O是坐标原点,如果△AOB是直角三角形,则△OAB的周长为 __ 。
已知二次函数y=-4x2-2mx+m2与反比例函数y= 的图像在第二象限内的一个交点的横坐标是-2,则m的值是__ 。
的图像在第二象限内的一个交点的横坐标是-2,则m的值是__ 。
有一个抛物线形拱桥,其最大高度为16m,跨度为40m,现把它的示意图放在平面直角坐标系中如 图(4),求抛物线的解析式是_______________。
如图(5),A、B、C是二次函数y=ax2+bx+c(a≠0)的图像上三点,根据图中给出的三点的位置,可得a_______0,c________0, ⊿________0.
老师给出一个函数,甲,乙,丙,丁四位同学各指出这个函数的一个性质:
甲:函数的图像不经过第三象限。乙:函数的图像经过第一象限。
丙:当x<2时,y随x的增大而减小。丁:当x<2时,y>0,
已知这四位同学叙述都正确,请构造出满足上述所有性质的一个函数____。
已知二次函数y=x2+bx+c的图像过点A(c,0),且关于直线x=2对称,则这个二次函数的解析式可能是_________________.(只要写出一个可能的解析式)
抛物线y=(x+2)2-3对称轴是( )
A x=-3 B x=3 C x=2 D x=-2
抛物线y=x2- x+a2的顶点在直线y=2上,则a的值为(
x+a2的顶点在直线y=2上,则a的值为( )
)
| A.-2 | B.2 | C.±2 | D.无法确定 |
二次函数y=ax2+c当x取x1 ,x2时,函数值相等,当x取x1+x2时,函数值为( )
A a+c B a-c C -c D c
抛物线y= x2的图像向左平移2个单位,在向下平移1个单位,得到的
x2的图像向左平移2个单位,在向下平移1个单位,得到的 函数解析式为
函数解析式为
A y= x2
x2  +2x-2 B y=
+2x-2 B y= x2+2x+1
x2+2x+1
C y= x2 -2x-1 D y=
x2 -2x-1 D y= x2 -2x+1
x2 -2x+1
已知(2,5)、 (4,5)是抛物线y=ax2+bx+c上的两点,则这个抛物线的对称轴方程是
A.x= . . |
B.x=2. | C.x=4. | D.x=3. |
已知函数y=ax2+bx+c的图象如图1所示,那么能正确反映函数y=ax+b图象的只可能是( )

如图,动点P从点A出发,沿线段AB运动至点B后,立即按原路返回,点P在运动过程中速度大小不变,则以点A为圆心,线段AP长为半径的圆 的面积S与点P的运动时间t之间的函数图象大致为( )
的面积S与点P的运动时间t之间的函数图象大致为( )
已知二次函数的图象经过原点及点( ,
, ),且图象与x轴的另一交点到原点的距离为1,则该二次函数的解析式为
),且图象与x轴的另一交点到原点的距离为1,则该二次函数的解析式为
抛物线 的部分图象如图所示,请写出与其关系式、图象相关的2个正确结论: , .(对称轴方程,图象与x正半轴、y轴交点坐标例外)
的部分图象如图所示,请写出与其关系式、图象相关的2个正确结论: , .(对称轴方程,图象与x正半轴、y轴交点坐标例外)
把抛物线y=ax +bx+c的图象先向右平移3个单位,再向下平移2个单位,所得的图象的解析式是y=x
+bx+c的图象先向右平移3个单位,再向下平移2个单位,所得的图象的解析式是y=x -3x+5
-3x+5 ,则a+b+c=__________
,则a+b+c=__________
二次函数 的图象如图所示,点
的图象如图所示,点 位于坐标原点, 点
位于坐标原点, 点 ,
, ,
, ,…,
,…, 在y轴的正半轴上,点
在y轴的正半轴上,点 ,
, ,
, ,…,
,…,  在二次函数
在二次函数
位于第一象限的图象上, 若△ ,△
,△ ,△
,△ ,…,△
,…,△
都为等边三角形,则△ 的边长=
的边长= 
已知二次函数y=- x2 –x+4回答下列问题
x2 –x+4回答下列问题
(1)用配方法将其化成y="a" (x-h)2+k的形式
(2)指出抛物线的顶点坐标和对称轴
(3)当x取何值时,y随x增大而增大;
当x取何值时,y随x增大而减小?
已知二次函 的图象过点(0, 5)
的图象过点(0, 5)
⑴ 求m的值,并写出二次函数的关系式;
⑵ 求出二次函数图象的顶点坐标、对称轴.
已知如图,二次函数y="ax2" +b x+c的图像过A、B、C三点
x+c的图像过A、B、C三点
观察图像写出A、B、C三点的坐标
求出二次函数的解析式
已知:o为坐标原点,∠ AOB=300 , ∠ABO=900 且A(2,0)求: 过A、B、O三点的二次函数解析式
 ,
, 为常数,当y达到最小值时,x的值为( )
为常数,当y达到最小值时,x的值为( ) ;
; ;
; ;
;


 =
= ,则x2+y2+z2的最小值为
,则x2+y2+z2的最小值为 ,当x=_________时,函数达到最小值
,当x=_________时,函数达到最小值
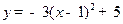 的顶点坐标为_______________________.
的顶点坐标为_______________________. 向上平移一个单位后,得以新的抛物线,那么新的抛物线的表达式是 .
向上平移一个单位后,得以新的抛物线,那么新的抛物线的表达式是 . 取得最大值时,
取得最大值时, ____________.
____________. _____________时
_____________时 ,二次函数
,二次函数 有最小值.
有最小值. 的图象关于原点O(0, 0)对称的图象的解析式是___。
的图象关于原点O(0, 0)对称的图象的解析式是___。 与
与 的两交点关于原点对称,则
的两交点关于原点对称,则 分别为 .
分别为 . 中,函数
中,函数 与自变量
与自变量 的部分对应值如下表:
的部分对应值如下表:







 2)当
2)当 ,
, 两点都在该函数的图象上,试比较
两点都在该函数的图象上,试比较 与
与 的大小.
的大小. 粤公网安备 44130202000953号
粤公网安备 44130202000953号