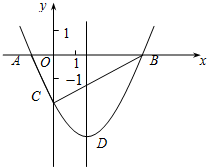如图,直线y=x+3与坐标轴分别交于A、B两点,抛物线 经过点A、B,顶点为C,连结CB并延长交x轴于点E,点D与点B关于抛物线的对称轴MN对称。
经过点A、B,顶点为C,连结CB并延长交x轴于点E,点D与点B关于抛物线的对称轴MN对称。
(1)求抛物线的解析式及顶点C的坐标;
(2)求证:四边形ABCD是直角梯形。
如图,抛物线y=ax2-4ax+c(a≠0)经过A(0,-1),B(5,0)两点,点P是抛物线上的一个动点 ,且位于直线AB的下方(不与A,B重合),过点P作直线PQ⊥x轴,交AB于点Q,设点P的横坐标为m.
,且位于直线AB的下方(不与A,B重合),过点P作直线PQ⊥x轴,交AB于点Q,设点P的横坐标为m.
(1)求a,c的值;
(2)设PQ的长为S,求S与m的函数关系式,写出m的取值范围;
(3)以PQ为直径的圆与抛物线的对称轴l有哪些位置关系?并写出对应的m取值范围.(不必写过程)
已知抛物线y=x2+4x+m(m为常数)
经过点(0,4).
(1) 求m的值;
(2) 将该抛物线先向右、再向下平移得到另一条抛物线.已知平移后的抛物线满足下述两个条件:它的对称轴(设为直线l2)与平移前的抛物线的对称轴(设为直线l1)关于y轴对称;它所对应的函数的最小值为-8.
① 试求平移后的抛物线的解析式;
② 试问在平移后的抛物线上是否存在点P,使得以3为半径的圆P既与x轴相切,又与直线l2相交?若存在,请求出点P的坐标,并求 出直线l2
出直线l2 被圆P所截得的弦AB的长度;若不存在,请说明理由.
被圆P所截得的弦AB的长度;若不存在,请说明理由.
如图,在平面直角坐标系中,抛物线y=x2+mx+n经过点A(3,0)、
B(0, -3),点P是直线AB上的动点,过点P作x轴的垂线
-3),点P是直线AB上的动点,过点P作x轴的垂线 交抛物线于点M,设点P的横
交抛物线于点M,设点P的横
坐标为t.
(1)分别求出直线AB和这条抛物线的解析式.
(2)若点P在第四象 限,连接AM、BM,当线段PM最长时,求△ABM的面积.
限,连接AM、BM,当线段PM最长时,求△ABM的面积.
(3)是否存在这样的点P,使得以点P、M、B、O为顶点的四边形为平行四边形?若存在,请直接写出点P的横坐标;若不存在,请说明理由.
(12分)如图,抛物线:y=ax2+bx+4与x轴交于点A(-2,0)和B(4,0)、与
y轴交于点C.
(1)求抛物线的解析式;
(2 )T是抛物线对称轴上的一点,且△ACT是以AC为底的等腰三角形,求点T的坐标;
)T是抛物线对称轴上的一点,且△ACT是以AC为底的等腰三角形,求点T的坐标;
(3)点M、Q分别从点A、B以每秒1个单位长度的速度沿x轴同时出发相向而行.当点M原点时,点Q立刻掉头并以每秒 个单位长度的速度向点B方向移动,当点M到达抛物线的对称轴时,两点停止运动.过点M的直线l⊥轴,交AC或BC于点P.求点M的运动时间t(秒)与△APQ的面积S的函数关系式,并求出S的最大值.
个单位长度的速度向点B方向移动,当点M到达抛物线的对称轴时,两点停止运动.过点M的直线l⊥轴,交AC或BC于点P.求点M的运动时间t(秒)与△APQ的面积S的函数关系式,并求出S的最大值.
(本题满分9分)
如图11,已知抛物线 与x 轴交于两点A、B,其顶点为C.
与x 轴交于两点A、B,其顶点为C.
(1)对于任意实数m,点M(m,-2)是否在该抛物线上?请说明理由;
(2)求证:△ABC是等腰直角三角形;
(3)已知点D在x轴上,那么在抛物线上是否存在点P,使得以B、C、D、P为顶点的四边形是 平行四边形?若存在,求点P的坐标;若不存在,请说明理由.
平行四边形?若存在,求点P的坐标;若不存在,请说明理由.
已知顶点为A(1,5)的抛物线 经过点B(5,1).
经过点B(5,1).
(1)求抛物线的解析式;
(2)如图(1),设C,D分别是 轴、
轴、 轴上的两个动点,求四边形ABCD周长的最小值;
轴上的两个动点,求四边形ABCD周长的最小值;
(3)在(2)中,当四边形ABCD的周长最小时,作直线CD.设点P( )(
)( )是直线
)是直线 上的一个动点,Q是OP的中点,以PQ为斜边按图(2)所示构造等腰直角三角形PRQ.
上的一个动点,Q是OP的中点,以PQ为斜边按图(2)所示构造等腰直角三角形PRQ.
①当△PBR与直线CD有 公共点时,求
公共点时,求 的取值范围;
的取值范围;
②在①的条件下,记△PBR与△COD的公共部分的面积为S.求S关于 的函数关系式,并求S的最大值。
的函数关系式,并求S的最大值。
(11·钦州).
如图,在平面直角坐标系中,抛物线与x轴交于A、B两点(A在B的左侧),与y轴交于点C (0,4),顶点为 .
.
(1)求抛物线的函数表达式;
(2)设抛物线的对称轴与轴交于点D,试在对称轴上找出点P,使△CDP为等腰三角形,请直接写出满足条件的所有点P的坐标.
(3)若点E是线段AB上的一个动点(与A、B不重合),分别连接AC、BC,过点E作EF∥AC交线段BC于点F,连接CE,记△CEF的面积为S,S是否存在最大值?若存在,求出S的最大值及此时E点的坐标;若不存在,请说明理由.
(11·柳州).
如图,一次函数y=-4x-4的图象与x轴、y轴分别交于A、C

(1)求抛物线的函数表达式;
(2)设抛物线的顶点为D,求四边形ABDC的面积;
(3)作直线MN平行于x轴,分别交线段AC、BC于点M、N.问在x轴上是否存在点P,使得△PMN是等腰直角三角形?如果存在,求出所有满足条件的P点的坐标;如果不存在,请说明理由.
已知二次函数的图象经过A(2,0)、C(0,12) 两点,且对称轴为直线x="4." 设
顶点为点P,与x轴的另一交点为点B.
(1)求二次函数的解析式及顶点P的坐标;
(2)如图1,在直线 y=2x上是否存在点D,使四边形OPBD为等腰梯形?若存在,求出点D的坐标;若不存在,请说明理由;
(3)如图2,点M是线段OP上的一个动点(O、P两点除外),以每秒 个单位长度的速度由点P向点O 运动,过点M作直线MN∥x轴,交PB于点N. 将△PMN沿直线MN对折,得到△P1MN. 在动点M的运动过程中,设△P1MN与梯形OMNB的重叠部分的面积为S,运动时间为t秒. 求S关于t的函数关系式.
个单位长度的速度由点P向点O 运动,过点M作直线MN∥x轴,交PB于点N. 将△PMN沿直线MN对折,得到△P1MN. 在动点M的运动过程中,设△P1MN与梯形OMNB的重叠部分的面积为S,运动时间为t秒. 求S关于t的函数关系式. 
已知抛物线y=ax2+bx+c与直线y=mx+n相交于两点,这两点的坐标分别是(0, )和
)和 (m-b,m2-mb+n),其中a,b,c
(m-b,m2-mb+n),其中a,b,c ,m,n为实数,且a,m不为0.
,m,n为实数,且a,m不为0.
(1)求c的值;
(2)设抛物线y=ax2+bx+c与x轴的两个交点是(x1,0)和(x2,0),求x1x2的值;
(3)当-1≤x≤1时,设抛物线y=ax2+bx+c上与x轴距离最大的点为P(xo,yo ),求这时|yo|的最小值.
抛物线y=ax2+bx+c与x轴的交点为A(m﹣4,0)和B(m,0),与直线y=﹣x+p相交于点A和点C(2m﹣4,m﹣6).
(1)求抛物线的解析式;
(2)若点P在抛物线上,且以点P和A,C以及另一点Q为顶点的平行四边形ACQP面积为12,求点P,Q的坐标;
(3)在(2)条件下,若点M是x轴下方抛物线上的动点,当△PQM的面积最大时,请求出△PQM的最大面积及点M的坐标.
已知二次函数 的图象与x轴分别交于点A、B,与y轴交于点C.点D是抛物线的顶点.
的图象与x轴分别交于点A、B,与y轴交于点C.点D是抛物线的顶点.
(1)如图①,连接AC,将△OAC沿直线AC翻折,若点O的对应点O'恰好落在该抛物
线的对称轴上,求实数a的值;
(2)如图②,在正方形EFGH中,点E、F的坐标分别是(4,4)、(4,3),边HG位于
边EF的右侧.小林同学经过探索后发现了一个正确的命题:“若点P是边EH或边HG上的
任意一点,则四条线段PA、PB、PC、PD不能与任何一个平行四边形的四条边对应相等(即
这四条线段不能构成平行四边形).”若点P是边EF或边FG上的任意一点,刚才的结论是
否也成立?请你积极探索,并写出探索过程;
(3)如图②,当点P在抛物线对称轴上时,设点P的纵坐标t是大于3的常数,试问:是
否存在一个正数a,使得四条线段PA、PB、PC、PD与一个平行四边形的四条边对应相等
(即这四条线段能构成平行四边形)?请说明理由.
已知:二次函数y=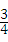 x2+bx+c,其图象对称轴为直线x=1,且经过点(2,﹣
x2+bx+c,其图象对称轴为直线x=1,且经过点(2,﹣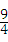 ).
).
(1)求此二次函数的解析式.
(2)设该图象与x轴交于B、C两点(B点在C点的左侧),请在此二次函数x轴下方的图象上确定一点E,使△EBC的面积最大,并求出最大面积.
注:二次函数y=ax2+bx+c(a≠0)的对称轴是直线x=﹣ .
.
如图,抛物线y=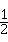 x2+bx﹣2与x轴交于A,B两点,与y轴交于C点,且A(﹣1,0).
x2+bx﹣2与x轴交于A,B两点,与y轴交于C点,且A(﹣1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M(m,0)是x轴上的一个动点,当MC+MD的值最小时,求m的值.