初中数学二次函数在给定区间上的最值解答题

如图，已知二次函数y=ax²+2x+c（a＞0）图象的顶点M在反比例函数上，且与x轴交于AB两点．
（1）若二次函数的对称轴为，试求a，c的值；
（2）在（1）的条件下求AB的长；
（3）若二次函数的对称轴与x轴的交点为N，当NO+MN取最小值时，试求二次函数的解析式．

如图：抛物线与x 轴交于A、B两点，点A的坐标是（1，0），与y轴交于点C。
⑴求抛物线的对称轴和点B的坐标；
⑵过点C作CP⊥对称轴于点P，连结BC交对称轴于点D，连结AC、BP，且 ，求抛物线的解析式；
⑶在⑵的条件下，设抛物线的顶点为G，连结BG、CG、求BCG的面积。

如图，已知二次函数 $y=x^2+bx+c$的图象的对称轴为直线 $x=1$，且与 $x$轴有两个不同的交点，其中一个交点坐标为 $(-1,0)$．
（1）求二次函数的关系式；
（2）在抛物线上有一点 $A$，其横坐标为-2，直线 $l$过点 $A$并绕着点 $A$旋转，与抛物线的另一个交点是点 $B$，点 $B$的横坐标满足 $﹣2＜x_B＜\frac{3}{2}$，当 $△AOB$的面积最大时，求出此时直线 $l$的关系式；
（3）抛物线上是否存在点 $C$使 $△AOC$的面积与（2）中 $△AOB$的最大面积相等．若存在，求出点 $C$的横坐标；若不存在说明理由．

如图，在平面直角坐标系中，O是坐标原点，点A的坐标是（﹣2，4），过点A作AB⊥y轴，垂足为B，连接OA．
（1）求△OAB的面积；
（2）若抛物线y=﹣x²﹣2x+c经过点A．
①求c的值；
②将抛物线向下平移m个单位，使平移后得到的抛物线顶点落在△OAB的内部（不包括△OAB的边界），求m的取值范围（直接写出答案即可）．

如图，二次函数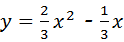的图象经过△AOB的三个顶点，其中A（﹣1，m），B（n，n）
（1）求A、B的坐标；
（2）在坐标平面上找点C，使以A、O、B、C为顶点的四边形是平行四边形．
①这样的点C有几个？
②能否将抛物线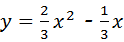平移后经过A、C两点，若能，求出平移后经过A、C两点的一条抛物线的解析式；若不能，说明理由．

已知一元二次方程x²－4x＋3=0的两根是m，n且m＜n.如图12，若抛物线y=-x²+bx
+c的图像经过点A（m，0）、B（0，n）.
（1）求抛物线的解析式.
（2）若（1）中的抛物线与x轴的另一个交点为C.根据图像回答，当x取何值时，抛物线的图像在直线BC的上方？
（3）点P在线段OC上，作PE⊥x轴与抛物线交与点E，若直线BC将△CPE的面积分成相等的两部分，求点P的坐标.

在等腰△ABC中，AB=AC=5，BC=6．动点M、N分别在两腰AB、AC上（M不与A、B重合，N不与A、C重合），且MN∥BC．将△AMN沿MN所在的直线折叠，使点A的对应点为P．
（1）当MN为何值时，点P恰好落在BC上？
（2）当MN=x，△MNP与等腰△ABC重叠部分的面积为y，试写出y与x的函数关系式．当x为何值时，y的值最大，最大值是多少？

如图，已知抛物线过点A（0，6），B（2，0），C（7，）．
（1）求抛物线的解析式；
（2）若D是抛物线的顶点，E是抛物线的对称轴与直线AC的交点，F与E关于D对称，求证：∠CFE=∠AFE；
（3）在y轴上是否存在这样的点P，使△AFP与△FDC相似，若有请求出所有和条件的点P的坐标，若没有，请说明理由．

如图，已知抛物线y=﹣x²+bx+9﹣b²（b为常数）经过坐标原点O，且与x轴交于另一点E．其顶点M在第一象限．
（1）求该抛物线所对应的函数关系式；
（2）设点A是该抛物线上位于x轴上方，且在其对称轴左侧的一个动点；过点A作x轴的平行线交该抛物线于另一点D，再作AB⊥x轴于点B．DE⊥x轴于点C．
①当线段AB、BC的长都是整数个单位长度时，求矩形ABCD的周长；
②求矩形ABCD的周长的最大值，并写出此时点A的坐标；
③当矩形ABCD的周长取得最大值时，它的面积是否也同时取得最大值？请判断井说明理由．

（11·曲靖）一名男生推铅球，铅球行进高度y（单位：m）与水平距离x


（1）求铅球推出的水平距离；
（2）通过计算说明铅球行进高度能否达到4m。

（11·兵团维吾尔）已知抛物线y＝－x²＋4x－3与x轴交于A、B两点（A
点在B点左侧），顶点为P．
（1）求A、B、P三点的坐标；
（2）在直角坐标系中，用列表描点法作出抛物线的图象，并根据图象写出x取何值时，函
数值大于零；
（3）将此抛物线的图象向下平移一个单位，请写出平称后图象的函数表达式．

（满分14分）如图（1），矩形ABCD的一边BC在直接 坐标系中x轴上，折叠边AD，使点D落在x轴上点F处，折痕为AE，已知AB=8，AD=10，并设点B坐标为（ ），其中 .
（1）求点E、F的坐标（用含的式子表示）；
（2）连接OA，若△OAF是等腰三角形，求 的值；
（3）如图（2），设抛物线 经过A、E两点，其顶点为M，连接AM，若∠OAM=90°，求 、 、 的值.

如图，已知二次函数 的图象经过
A（ ， ），B（0,7）两点．
⑴ 求该抛物线的解析式及对称轴；
⑵ 当 为何值时， ？
⑶ 在 轴上方作平行于 轴的直线 ，与抛物线交于C，D两点（点C在对称轴的左侧），
过点C，D作 轴的垂线，垂足分别为F，E．当矩形CDEF为 正方形时，求C点的坐标．

如图，矩形OABC中，点O为原点，点A的坐标为（0，8），点C的坐标为（6，0）．抛物线经过A、C两点，与AB边交于点D．
（1）求抛物线的函数表达式；
（2）点P为线段BC上一个动点（不与点C重合），点Q为线段AC上一个动点，AQ=CP，连接PQ，设CP=m，△CPQ的面积为S．
①求S关于m的函数表达式，并求出m为何值时，S取得最大值；
②当S最大时，在抛物线的对称轴l上若存在点F，使△FDQ为直角三角形，请直接写出所有符合条件的F的坐标；若不存在，请说明理由．

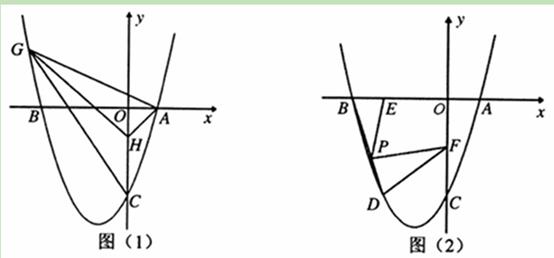
（11·十堰）12分）如图，已知抛物线y=x2+bx+c与x轴交于点A（1，0）和点B，与y轴交于点C（0，-3）。
（1）求抛物线的解析式；
（2）如图（1），已知点H（0，-1）.问在抛物线上是否存在点G（点G在y轴的左侧），使得S_△GHC=S_△GHA？若存在，求出点G的坐标，若不存在，请说明理由；
（3）如图（2），抛物线上点D在x轴上的正投影为点E（-2，0），F是OC的中点，连接DF，P为线段BD上的一点，若∠EPF=∠BDF，求线段PE的长.