2011年初中毕业升学考试(山东济南卷)数学解析版
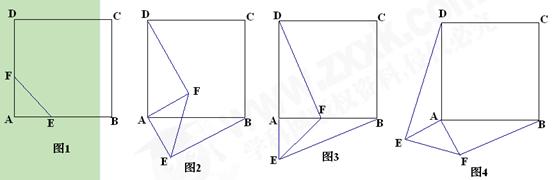
已知:正方形ABCD.
(1)如图1,点E、点F分别在边
和
上,且
.此时,线段
、
的数量关 系和位置关系分别是什么?请直接写出结论.
系和位置关系分别是什么?请直接写出结论.
(2)如图2,等腰直角三角形FAE绕直角顶点A顺时针旋转
,当
时,连接
、
,此时(1)中结论是否成立,如果成立,请证明;如果不成立,请说明理由.
(3)如图3,等腰直角三 角形FAE绕直角顶点A顺时针旋转
,当
时,连接
、
,猜想当
与
满足什么数量关系时,直线
垂直平分
.请直接写出结论.
角形FAE绕直角顶点A顺时针旋转
,当
时,连接
、
,猜想当
与
满足什么数量关系时,直线
垂直平分
.请直接写出结论.
(4)如图4,等腰直角三角形FAE绕直角顶点A顺时针旋转
,当
时,连接
、
、
、
得到四边形
,则顺次连接四边形
各边中点所组成的四边形是什么特殊四边形?请直接写出结论.
(11·丹东)(本题14分)已知:二次函数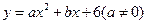 与
与 轴交于A,B两点(点A在点B的左侧),点A、点B的横坐标是一元二次方程
轴交于A,B两点(点A在点B的左侧),点A、点B的横坐标是一元二次方程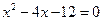 的两个根.
的两个根.
(1)请直接写出点A、点B的坐标.
(2)请求出该二次函数表达式及对称轴和顶点坐标.
(3)如图1,在二次函数对称轴上是否存在点P,使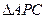 的周长最小,若存在
的周长最小,若存在 ,请求出点P的坐标;若不存在,请说明理由.
,请求出点P的坐标;若不存在,请说明理由.
(4)如图2,连接AC、BC,点Q是线段OB上一个动点(点Q不与点O、B重合). 过点Q作QD∥AC交于BC点D,设Q点坐标(m,0),当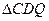 面积S最大时,求m的值.
面积S最大时,求m的值.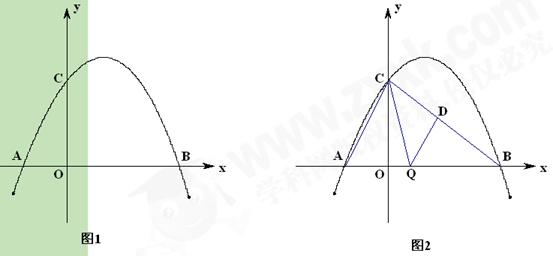
(11·十堰)据统计,十堰市2011年报名参加九年级学业考试总人数为26537人,则26537用科学记数法表示为(保留两个有效数字)( )
| A.2.6×104 | B.2.7×104 | C.2.6×105 | D.2.7×105 |
(11·十堰)如图,Rt△ABC中,∠ACB=90°,DE过点C,且DE//AB,若∠ACD=500,则∠B的度数是( )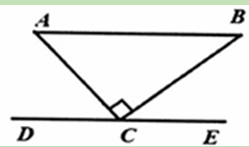
| A.50° | B.40° | C.30° | D.25° |
(11·十堰)工人师傅常用角尺平分一个任意角。做法如下:如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合。过角尺顶点C作射线OC。由做法得△MOC≌△NOC的依据是( )
A.AAS B.SAS C.ASA D.SSS
(11·十堰)现有边长相同的正三角、正方形和正六边形纸片若干张,下列拼法中不能镶嵌成一个平面图案的是( )
| A.正方形和正六边形 | B.正三角形和正方形 |
| C.正三角形和正六边形 | D.正三角形、正方形和正六边形 |
(11·十堰)如图,在网格中有一个直角三角形(网格中的每个小正方形的边长均为1个单位长度),若以该三角形一边为公共边画一个新三角形与原来的直角三角形一起组成一个等腰三角形,要求新三角形与原来的直角三角形除了有一条公共边外,没有其它的公共点,新三角形的顶点不一定在格点上,那么符合要求的新三角形有( )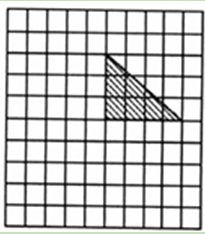
| A.4个 | B.6个 | C.7个 | D.9个 |
(11·十堰)如图所示为一个污水净化塔内部,污水从上方入口进入后流经形如等腰直角三角形的净化材料表面,流向如图中箭头所示,每一次水流流经三角形两腰的机会相同,经过四层净化后流入底部的5个出口中的一个。下列判断:①5个出口的出水量相同;②2号出口的出水量与4号出口的出水量相同;③1,2,3号出水口的出水量之比约为1:4:6;④若净化材料损耗速度与流经其表面水的数量成正比,则更换最慢一个三角形材料使用的时间约为更换一个三角形材料使用时间的8倍,其中正确的判断有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
(11·十堰)如图等腰梯形ABCD中,AD//BC,AB//DE,BC=8,AB=6,AD=5,则△CDE的周长是 .
(11·十堰)如图,平行四边形AOBC中,对角线交于点E,双曲线 (k>0)经过A、E两点,若平行四边形AOBC的面积为18,则k= .
(k>0)经过A、E两点,若平行四边形AOBC的面积为18,则k= .
(11·十堰)今年我省部分地区遭遇严重干旱,为鼓励市民节约用水,我市自来水公司按分段收费标准收费,右图反映的是每月收水费y(元)与用水量x(吨)之间的函数关系。
(1)小聪家五月份用水7吨,应交水费 元;
(2)按上述分段收费标准,小聪家三、四月份分别交水费29元和19.8元,问四月份比三月份节约用水多少吨?
(11·十堰)为纪念辛亥革命100周年,某校八年级(1)班全体学生举行了“首义精神耀千秋”知识竞赛。根据竞赛成绩(得分为整数,满分为100分)绘制了频数分布直方图(如图所示),根据频数分布直方图解答下列问题: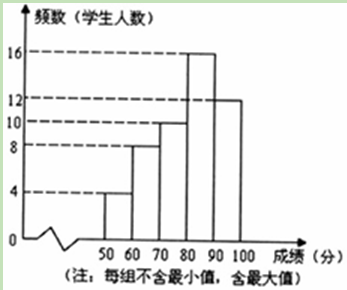
(1)求该班的学生人数;
(2)若成绩不少于80分为优秀,且该班有3名学生的成绩为80分,则学生成绩的优秀率是多少?
(3)若该班超过82分的学生有22人,则学生成绩的中位数可能是多少分?(直接写出答案即可)
(11·十堰)请阅读下列材料:
问题:已知方程x2+x-1=0,求一个一元二次方程,使它的根分别是已知方程根的2倍。
化简,得y2+2y-4=0.
故所求方程为y2+2y-4=0。
这种利用方程根的代换求新方程的方法,我们称为“换根法”。
请用阅读材料提供的“换根法”求新方程(要求:把所求方程化为一般形式);
(1)已知方程x2+x-2=0,求一个一元二次方程,使它的根分别是已知方程根的相反数,则所求方程为: ;
(2)已知关于x的一元二次方程ax2+bx+c=0(a≠0)有两个不等于零的实数根,求一个一元二次方程,使它的根分别是已知方程根的倒数。
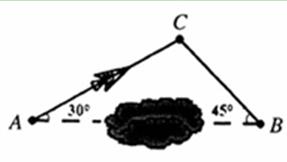
(11·十堰)如图,一架飞机从A地飞往B地,两地相距600km.飞行员为了避开某一区域的雷雨去层,从机场起飞以后,就沿与原来的飞行方向成300 角的方向飞行,飞行到中途,再沿与原来的飞行方向成450角的方向继续飞行直到终
角的方向飞行,飞行到中途,再沿与原来的飞行方向成450角的方向继续飞行直到终 点。这样飞机的飞行路程比原来的路程控交换机600km远了多少?
点。这样飞机的飞行路程比原来的路程控交换机600km远了多少?
(11·十堰)A,B两地间的距离为15千米,甲从A地出发步行前往B地,20分钟后,乙从B地出发骑车前往A地,且乙骑车比甲步行每小时多走10千米。乙到达A地后停 留40分钟,然后骑车按原路原速返回,结果甲、乙两人同时到达B地。请你就“甲从A地到B地步行所用时间”或“甲步行的速度”提出一个用分式方程解决的问题,并写出解题过程。
留40分钟,然后骑车按原路原速返回,结果甲、乙两人同时到达B地。请你就“甲从A地到B地步行所用时间”或“甲步行的速度”提出一个用分式方程解决的问题,并写出解题过程。
(11·十堰)如图,AB是半圆O的直径,点C为半径OB上一点,过点C作CD⊥AB交半圆O于点D,将△ACD沿AD折叠 得到△AED,AE交半圆于点F,连接DF。
得到△AED,AE交半圆于点F,连接DF。
(1)求证:DE是半圆的切线;
(2)连接OD,当OC=BC时,判断四边形ODFA的形状,并证明你的结论。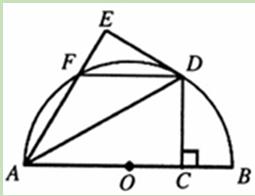
(11·十堰)如图,线段AD=5,⊙A的半径为1,C为⊙A上一动点,CD的垂直平分线分别交CD于点E,B,连接BC,AC,构成△ABC,设AB=x.
(1)求x的取值范围;
(2)若△ABC为直角三角形,则x= ;
(3)设△ABC的面积的平方为W,求W的最大值。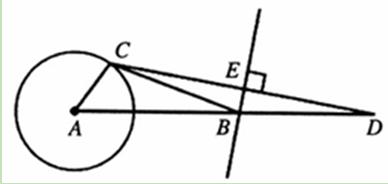
(11·十堰)12分)如图,已知抛物线y=x2+bx+c与x轴交于点A(1,0)和点B,与y轴交于点C(0,-3)。
(1)求抛物线的解析式;
(2)如图(1),已知点H(0,-1).问在抛物线上是否存在点G(点G在y轴的左侧),使得S△GHC=S△GHA?若存在,求出点G的坐标,若不存在,请说明理由;
(3)如图(2),抛物线上点D在x轴上的正投影为点E(-2,0),F是OC的中点,连接DF,P为线段BD上的一点,若∠EPF=∠BDF,求线段PE的长.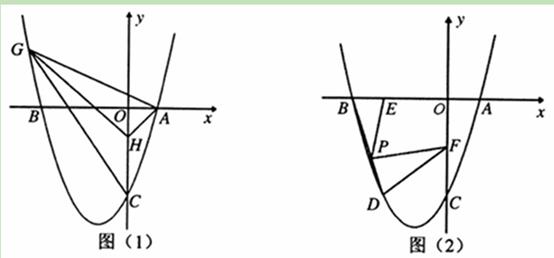
“山东半岛蓝色经济区”规划主体区包括的海域面积共159500平方公里.159500用科学记数法表示为( )
| A.1595×102 | B.159.5×103 | C.15.95×104 | D.1.595×105 |
某校九年级一班体育委员在一次体育课上记录了六位同学托排球的个数分别为37,25,30,35,28,25,这组数据的中位数为( )
| A.25 | B.28 | C.29 | D.32.5 |
下列运算正确的是( )
| A.a2•a3=a6 | B.(a2)3=a6 | C.a6÷a2=a3 | D.2﹣3=﹣6 |
某校为举办“庆祝建党90周年”的活动,从全校1400名学生中随机调查了280名学生,其中有80人希望举办文艺演出,据此估计该学校希望举办文艺演出的学生人数为( )
| A.1120 | B.400 | C.280 | D.80 |
一次函数y=(k﹣2)x+3的图象如图所示,则k的取值范围是( )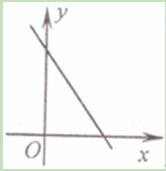
| A.k>2 | B.k<2 | C.k>3 | D.k<3 |
如图,在等腰梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,下列结论不一定正确的是( )
A.AC="BD " B.∠OBC=∠OCB
C.S△AOB=S△DOC D.∠BCD=∠BDC
如图,O为原点,点A的坐标为(3,0),点B的坐标为(0,4),⊙D过A、B、O三点,点C为 上一点(不与O、A两点重合),则cosC的值为( )
上一点(不与O、A两点重合),则cosC的值为( )
A. B.
B. C.
C. D.
D.
竖直向上发射的小球的高度h(m)关于运动时间t(s)的函数表达式为h=at2+bt,其图象如图所示,若小球在发射后第2秒与第6秒时的高度相等,则下列时刻中小球的高度最高的是( )
| A.第3秒 | B.第3.5秒 | C.第4.2秒 | D.第6.5秒 |
观察下列各式:
(1)1=12;(2)2+3+4=32;(3)3+4+5+6+7=52;(4)4+5+6+7+8+9+10=72…
请你根据观察得到的规律判断下列各式正确的是( )
| A.1005+1006+1007+…+3016=20112 | B.1005+1006+1007+…+3017=20112 |
| C.1006+1007+1008+…+3016=20112 | D.1007+1008+1009+…+3017=20112 |
如图,
中,
,
,分别以
的边
、
、
为一边向
外作正方形
、
、
,连接
、
、
,设
、
、
的面积分别为
、
、
,则下列结论正确的是( )

| A. |
|
B. |
|
| C. |
|
D. |
|
如图,矩形ABCD的边AB与y轴平行,顶点A的坐标为(1,2),点B与点D在反比例函数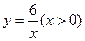 的图象上,则点C的坐标为 .
的图象上,则点C的坐标为 .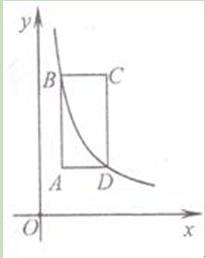
如图,△ABC为等边三角形,AB=6,动点O在△ABC的边上从点A出发沿着A→C→B→A的路线匀速运动一周,速度为1个长度单位每秒,以O为圆心、 为半径的圆在运动过程中与△ABC的边第二次相切时是出发后第 秒.
为半径的圆在运动过程中与△ABC的边第二次相切时是出发后第 秒.
(1)如图1,△ABC中,∠A=60°,∠B:∠C=1:5,求∠B的度数.
(2)如图2,点M为正方形ABCD对角线BD上一点,分别连接AM、CM.求证:AM=CM.
某小学在6月1日组织师生共110人到趵突泉公园游览,趵突泉公园规定:成人票价每位40元,学生票价每位20元.该学校购票共花费2400元,在这次游览活动中,教师和学生各有多少人?
飞飞和欣欣两位同学到某文具专卖店购买文具,恰好赶上“店庆购物送礼”活动,该文具店设置了A、B、C、D四种型号的钢笔作为赠品,购物者可随机抽取一支,抽到每种型号钢笔的可能性相同.
(1)飞飞购物后,获赠A型号钢笔的概率是多少?
(2)飞飞和欣欣购物后,两人获赠的钢笔型号相同的概率是多少?
如图1,△ABC中,∠C=90°,∠ABC=30°,AC=m,延长CB至点D,使BD=AB.
①求∠D的度数;
②求tan75°的值.
(2)如图2,点M的坐标为(2,0),直线MN与y轴的正半轴交于点N,∠OMN=75°.求直线MN的函数表达式.
如图,矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线 经过A、C两点,与AB边交于点D.
经过A、C两点,与AB边交于点D.
(1)求抛物线的函数表达式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式,并求出m为何值时,S取得最大值;
②当S最大时,在抛物线 的对称轴l上若存在点F,使△FDQ为直角三角形,请直接写出所有符合条件的F的坐标;若不存在,请说明理由.
的对称轴l上若存在点F,使△FDQ为直角三角形,请直接写出所有符合条件的F的坐标;若不存在,请说明理由.
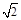

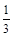
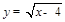 中自变量x的取值范围是( )
中自变量x的取值范围是( )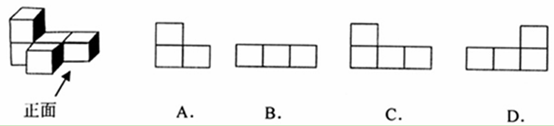
 的解是正整数,则整数P的值为 。
的解是正整数,则整数P的值为 。 的圆经过一个半径为4的圆的圆心,则图中阴影部分的面积为 。
的圆经过一个半径为4的圆的圆心,则图中阴影部分的面积为 。
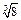 -2-1+︱
-2-1+︱ -1︱.
-1︱.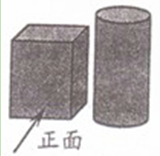

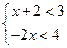 的解集是( )
的解集是( )

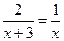 .
.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号