2011年初中毕业升学考试(湖北十堰卷)数学
某次器乐比赛共有11名选手参加,且他们的得分都互不相同.现在知道这次比赛
按选手得分由高到低的顺序设置了6个获奖名额.若已知某位选手参加这次比赛的得分,要
判断他能否获奖,则在下列描述选手比赛成绩的统计量中,只需知道
| A.方差 | B.平均数 |
| C.众数 | D.中位数 |
如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,∠CDB=30°,⊙O的半径为 cm,
cm,
则弦CD的长为
A. cm cm |
B.3cm |
C. cm cm |
D.9cm |

若m ― n = 4,则2m2― 4mn + 2n2的值为
| A.32 | B.22 |
| C.12 | D.0 |
根据下表中的二次函数 的自变量x与函数y的对应值,可判断该
的自变量x与函数y的对应值,可判断该
二次函数的图象与x轴
| x |
… |
-1 |
0 |
1 |
2 |
… |
||||
| y |
… |
-1 |
 |
-2 |
 |
…
|
如图,正方形 的边长为2, 将长为2的线段
的边长为2, 将长为2的线段 的两端放在正方形相邻的
的两端放在正方形相邻的
两边上同时滑动.如果点 从点
从点 出发,沿图中所示方向按
出发,沿图中所示方向按 滑动到点
滑动到点
为止,同时点 从点
从点 出发,沿图中所示方向按
出发,沿图中所示方向按 滑动到点
滑动到点 为止,那
为止,那
么在这个过程中,线段 的中点
的中点 所经过的路线围成的图形的面积为
所经过的路线围成的图形的面积为
A.4- |
B. |
| C.2 | D. |

如图,BD是平行四边形ABCD的对角线,点E、F在BD上,要使四边形AECF是平行四边形,还需增加的一个条件是 (填一种情况即可).
某校为了解九年级学生体育测试情况,以九年级(1)班学生的体育测试成绩为
样本,按A,B,C,D四个等级进行统计,并将统计结果绘制成如下的统计 图,请你结
合图中所给信息解答下列问题:
(说明:A级:90分~100分;B级:75分~89分;C级:60分~74分;D级:60分以下)
①样本中D级学生有 人;
②扇形统计图中A级所在的扇形的圆心角度数是 ;
③若该校九年级有500名学生,请你用此样本估计体育测试中A级和B级的学生人数约为 人.
如图,已知双曲线 经过直角三角形OAB斜边OA的中点D,且与
经过直角三角形OAB斜边OA的中点D,且与
直角边AB相交于点C.若点A的坐标为( ,4),则△AOC的面积为 .
,4),则△AOC的面积为 .
如图1,把一张标准纸一次又一次对开,得到“2开”纸、“4开”纸、“8开”纸、“16
开”纸……已知标准纸的短边长为 .
.
(Ⅰ)如图2,把上面对开得到的“16开”纸按如下步骤折叠:
第一步:将矩形的短边AB与长边AD对齐折叠,点B落在AD上的点B′处,铺平后得折痕AE;
第二步:将长边AD与折痕AE对齐折叠,点D正好与点E重合,铺平后得折痕AF.则AD:AB的值是 .
(Ⅱ)求“2开”纸长与宽的比__________.
(Ⅲ)如图3,由8个大小相等的小正方形构成“L”型图案,它的四个顶点E、F、G、H分别在“16开”纸的边AB、BC、CD、DA上,则DG的长为__________.
(本小题8分)已知反比例函数 的图象经过点A(1,3).
的图象经过点A(1,3).
求:(Ⅰ)m的值和这个函数的解析式;
(Ⅱ)当-3< <-1时,对应的函数
<-1时,对应的函数 的取值范围.
的取值范围.
(本小题8分)某市今年中考物理、化学实验操作考试,采用学生抽签方式决定自己的考试内容,规定:每位考生必须在三个物理实验(用纸签A、B、C表示)和三个化学实验(用纸签D、E、F表示)中各抽取一个进行考试.小刚在看不到纸签的情况下,分别从中各随机抽取一个.
(Ⅰ)采用树形图法(或列表法)表示所有可能出现的结果;
(Ⅱ)小刚抽到物理实验B和化学实验F(记作事件M)的概率是多少?
(本小题8分)如图,四边形ABCD内接于⊙O,BD是⊙O的直径,
AE⊥CD于点E,DA平分∠BDE.
(Ⅰ)求证:AE是⊙O的切线;
(Ⅱ)若∠DBC=30°,DE="1" cm,求BD的长.
(本小题8分)如图,线段AB、DC分别表示甲、乙两建筑物的高, ,
, ,从B点测得D点的仰角
,从B点测得D点的仰角 为60°,从A点测得D点
为60°,从A点测得D点
的仰角 为30°,已知甲建筑物高AB=36米.
为30°,已知甲建筑物高AB=36米.
(Ⅰ)求乙建筑物的高DC;
(Ⅱ)求甲、乙两建筑物之间的距离BC(结果精确到0.01米).(参考数据: )
)
(本小题8分)注意:为了使同学们更好地解答本题,我们提供了一种解题思路,你可以依照这个思路按下面的要求填空,完成本题的解答.也可以选用其他的解题方案,此时不必填空,只需按照解答题的一般要求进行解答.
有一工程需在规定日期内完成,如果甲单独工作刚好能够按期完成;如果乙单独工作就要超过规定日期3天. 现在甲、乙合作2天后余下的工程由乙单独完成刚好在规定日期完成,求规定日期是几天?
解题方案:
设规定的日期为x天,
(Ⅰ)用含x的代数式表示:
①甲的工作效率为 ;
②乙的工作效率为 ;
(Ⅱ)根据题意,列出相应方程 ;
(Ⅲ)解这个方程,得 ;
(Ⅳ)检验: ;
(Ⅴ)答:规定日期是 .
如图,四边形 是正方形, 是等边三角形, 为对角线 (不含B点)上任意一点,将 绕点 逆时针旋转60°得到BN,连接
(Ⅰ)求证:
;
(Ⅱ)①当M点在何处时,
的值最小;
②当M点在何处时,
的值最小,并说明理由;
(Ⅲ)当
的最小值为
时,求正方形的边长.


(本小题10分)在平面直角坐标系中,将直线l: 沿x轴翻折,得到一条新直线与x轴交于点A,与y轴交于点B,将抛物线
沿x轴翻折,得到一条新直线与x轴交于点A,与y轴交于点B,将抛物线 :
: 沿x轴平移,得到一条新抛物线
沿x轴平移,得到一条新抛物线 与y轴交于点D,与直线AB交于点E、点F.
与y轴交于点D,与直线AB交于点E、点F.
(Ⅰ)求直线AB的解析式;
(Ⅱ)若线段DF∥x轴,求抛物线 的解析式;
的解析式;
(Ⅲ)在(2)的条件下,若点F在y轴右侧,过F作FH⊥x轴于点G,与直线l交于点H,一条直线m(m不过△AFH的顶点)与AF交于点M,与FH交于点N,如果直线m既垂直于直线AB又平分△AFH的面积,求直线m的解析式.
(11·十堰)据统计,十堰市2011年报名参加九年级学业考试总人数为26537人,则26537用科学记数法表示为(保留两个有效数字)( )
| A.2.6×104 | B.2.7×104 | C.2.6×105 | D.2.7×105 |
(11·十堰)如图,Rt△ABC中,∠ACB=90°,DE过点C,且DE//AB,若∠ACD=500,则∠B的度数是( )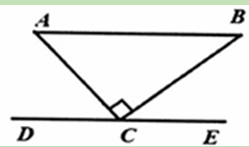
| A.50° | B.40° | C.30° | D.25° |
(11·十堰)工人师傅常用角尺平分一个任意角。做法如下:如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合。过角尺顶点C作射线OC。由做法得△MOC≌△NOC的依据是( )
A.AAS B.SAS C.ASA D.SSS
(11·十堰)现有边长相同的正三角、正方形和正六边形纸片若干张,下列拼法中不能镶嵌成一个平面图案的是( )
| A.正方形和正六边形 | B.正三角形和正方形 |
| C.正三角形和正六边形 | D.正三角形、正方形和正六边形 |
(11·十堰)如图,在网格中有一个直角三角形(网格中的每个小正方形的边长均为1个单位长度),若以该三角形一边为公共边画一个新三角形与原来的直角三角形一起组成一个等腰三角形,要求新三角形与原来的直角三角形除了有一条公共边外,没有其它的公共点,新三角形的顶点不一定在格点上,那么符合要求的新三角形有( )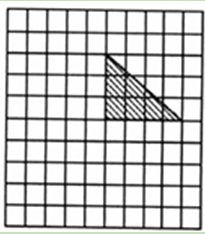
| A.4个 | B.6个 | C.7个 | D.9个 |
(11·十堰)如图所示为一个污水净化塔内部,污水从上方入口进入后流经形如等腰直角三角形的净化材料表面,流向如图中箭头所示,每一次水流流经三角形两腰的机会相同,经过四层净化后流入底部的5个出口中的一个。下列判断:①5个出口的出水量相同;②2号出口的出水量与4号出口的出水量相同;③1,2,3号出水口的出水量之比约为1:4:6;④若净化材料损耗速度与流经其表面水的数量成正比,则更换最慢一个三角形材料使用的时间约为更换一个三角形材料使用时间的8倍,其中正确的判断有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
(11·十堰)如图等腰梯形ABCD中,AD//BC,AB//DE,BC=8,AB=6,AD=5,则△CDE的周长是 .
(11·十堰)如图,平行四边形AOBC中,对角线交于点E,双曲线 (k>0)经过A、E两点,若平行四边形AOBC的面积为18,则k= .
(k>0)经过A、E两点,若平行四边形AOBC的面积为18,则k= .
(11·十堰)今年我省部分地区遭遇严重干旱,为鼓励市民节约用水,我市自来水公司按分段收费标准收费,右图反映的是每月收水费y(元)与用水量x(吨)之间的函数关系。
(1)小聪家五月份用水7吨,应交水费 元;
(2)按上述分段收费标准,小聪家三、四月份分别交水费29元和19.8元,问四月份比三月份节约用水多少吨?
(11·十堰)为纪念辛亥革命100周年,某校八年级(1)班全体学生举行了“首义精神耀千秋”知识竞赛。根据竞赛成绩(得分为整数,满分为100分)绘制了频数分布直方图(如图所示),根据频数分布直方图解答下列问题: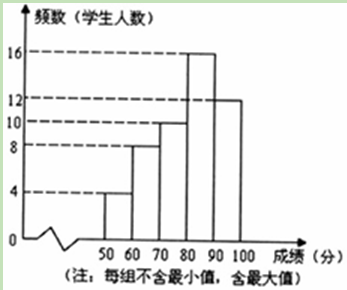
(1)求该班的学生人数;
(2)若成绩不少于80分为优秀,且该班有3名学生的成绩为80分,则学生成绩的优秀率是多少?
(3)若该班超过82分的学生有22人,则学生成绩的中位数可能是多少分?(直接写出答案即可)
(11·十堰)请阅读下列材料:
问题:已知方程x2+x-1=0,求一个一元二次方程,使它的根分别是已知方程根的2倍。
化简,得y2+2y-4=0.
故所求方程为y2+2y-4=0。
这种利用方程根的代换求新方程的方法,我们称为“换根法”。
请用阅读材料提供的“换根法”求新方程(要求:把所求方程化为一般形式);
(1)已知方程x2+x-2=0,求一个一元二次方程,使它的根分别是已知方程根的相反数,则所求方程为: ;
(2)已知关于x的一元二次方程ax2+bx+c=0(a≠0)有两个不等于零的实数根,求一个一元二次方程,使它的根分别是已知方程根的倒数。
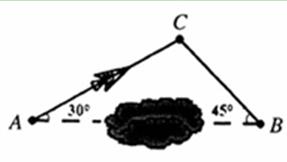
(11·十堰)如图,一架飞机从A地飞往B地,两地相距600km.飞行员为了避开某一区域的雷雨去层,从机场起飞以后,就沿与原来的飞行方向成300 角的方向飞行,飞行到中途,再沿与原来的飞行方向成450角的方向继续飞行直到终
角的方向飞行,飞行到中途,再沿与原来的飞行方向成450角的方向继续飞行直到终 点。这样飞机的飞行路程比原来的路程控交换机600km远了多少?
点。这样飞机的飞行路程比原来的路程控交换机600km远了多少?
(11·十堰)A,B两地间的距离为15千米,甲从A地出发步行前往B地,20分钟后,乙从B地出发骑车前往A地,且乙骑车比甲步行每小时多走10千米。乙到达A地后停 留40分钟,然后骑车按原路原速返回,结果甲、乙两人同时到达B地。请你就“甲从A地到B地步行所用时间”或“甲步行的速度”提出一个用分式方程解决的问题,并写出解题过程。
留40分钟,然后骑车按原路原速返回,结果甲、乙两人同时到达B地。请你就“甲从A地到B地步行所用时间”或“甲步行的速度”提出一个用分式方程解决的问题,并写出解题过程。
(11·十堰)如图,AB是半圆O的直径,点C为半径OB上一点,过点C作CD⊥AB交半圆O于点D,将△ACD沿AD折叠 得到△AED,AE交半圆于点F,连接DF。
得到△AED,AE交半圆于点F,连接DF。
(1)求证:DE是半圆的切线;
(2)连接OD,当OC=BC时,判断四边形ODFA的形状,并证明你的结论。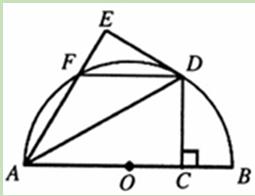
(11·十堰)如图,线段AD=5,⊙A的半径为1,C为⊙A上一动点,CD的垂直平分线分别交CD于点E,B,连接BC,AC,构成△ABC,设AB=x.
(1)求x的取值范围;
(2)若△ABC为直角三角形,则x= ;
(3)设△ABC的面积的平方为W,求W的最大值。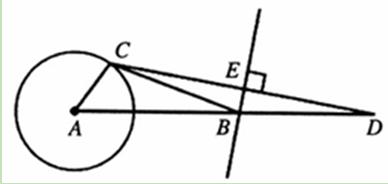


 的点可能是
的点可能是 
 为实数,且
为实数,且 >1
>1 <0
<0 >1
>1 >1
>1 的值为0,则
的值为0,则 的值为_____________.
的值为_____________. 



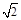

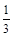
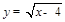 中自变量x的取值范围是( )
中自变量x的取值范围是( )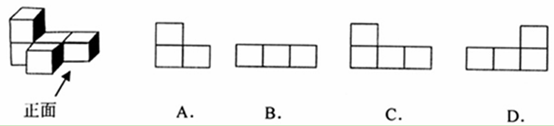
 的解是正整数,则整数P的值为 。
的解是正整数,则整数P的值为 。 的圆经过一个半径为4的圆的圆心,则图中阴影部分的面积为 。
的圆经过一个半径为4的圆的圆心,则图中阴影部分的面积为 。
 -2-1+︱
-2-1+︱ -1︱.
-1︱.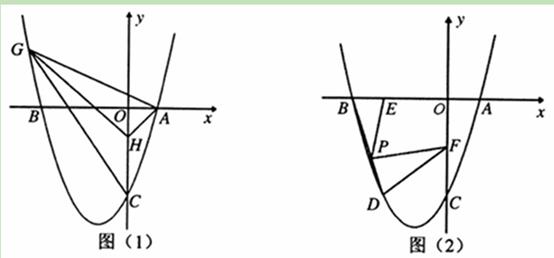
 粤公网安备 44130202000953号
粤公网安备 44130202000953号