如图,抛物线y=x2+bx+c与x轴交于A(-1,0)和B(3,0)两点,交y轴于E.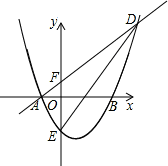
(1)求此抛物线的表达式.
(2)若直线y=x+1与抛物线交于A,D两点,与y轴交于点F,连接DE,求△DEF的面积.
如图,已知二次函数 的图像经过A(-1,-1),C(1,3).
的图像经过A(-1,-1),C(1,3).
(1)求二次函数的解析式并画出它的图像;
(2)直接写出点A关于抛物线对称轴的对称点A'的坐标;
(3)求该抛物线上到x轴的距离为2的所有点的坐标.
二次函数y=ax2+c (a≠0)的图象经过点A(1,-1),B(2,5),
(1)求函数y=ax2+c的表达式。
(2)若点C(-2,m),D(n ,7)也在函数的图象上,求点C的坐标;点D的坐标。
已知抛物线抛物线y n=-(x-an)2+an(n为正整数,且0<a1<a2<…<an)与x轴的交点为An-1(bn-1,0)和An(bn,0),当n=1时,第1条抛物线y1=-(x-a1)2+a1与x轴的交点为A0(0,0)和A1(b1,0),其他依此类推.
(1)求a1,b1的值及抛物线y2的解析式;
(2)抛物线y3的顶点坐标为( , );
依此类推第n条抛物线yn的顶点坐标为( , );
所有抛物线的顶点坐标满足的函数关系是 ;
(3)探究下列结论:
若用An-1An表示第n条抛物线被x轴截得得线段长,直接写出A0A1的值,并求出An-1An;
如图,平面直角坐标系中,以点C(2, )为圆心,以2为半径的圆与x轴交于A,B两点.
)为圆心,以2为半径的圆与x轴交于A,B两点.
(1)求A,B两点的坐标;
(2)若二次函数y=x2+bx+c的图象经过点A,B,试确定此二次函数的解析式.
二次函数 中x、y满足下表:
中x、y满足下表:
| x |
…… |
-1 |
0 |
1 |
2 |
3 |
…… |
| y |
…… |
0 |
-3 |
-4 |
-3 |
m |
…… |
(1)求这个二次函数的解析式;
(2)求m=?
(本题8分)已知二次函数 的图象经过点A(2, -3),B(-1,12).
的图象经过点A(2, -3),B(-1,12).
(1)求这个二次函数的解析式;
(2)求这个图象的顶点坐标和对称轴
(本小题满分8分)已知二次函数的图象经过点( -1,-8 ),顶点为( 2, 1 ).
(1)求这个二次函数的表达式;
(2)分别求图象与x轴、y轴的交点坐标.