已知二次函数y=x2-2mx+m2-1.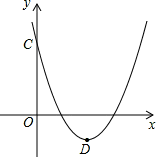
(1)当二次函数的图象经过坐标原点O(0,0)时,求二次函数的解析式;
(2)如图,当m=2时,该抛物线与y轴交于点C,顶点为D,求C、D两点的坐标;
(3)在(2)的条件下,x轴上是否存在一点P,使得PC+PD最短?若P点存在,求出P点的坐标;若P点不存在,请说明理由.
(本题8分)为了改善小区环境,某小区决定要在一块一边靠墙(墙长25m)的空地上修建一个矩形绿化带ABCD,绿化带一边靠墙,另三边用总长为40m的栅栏围住(如图).若设绿化带的BC边长为x m,绿化带的面积为y m2.
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)当x为何值时,满足条件的绿化带的面积最大.
如图,在平面直角坐标系中,已知点A(0,1)、B(3,5),以AB为边作如图所示的正方形ABCD,顶点在坐标原点的抛物线恰好经过点D,P为抛物线上的一动点.
(1)直接写出点D的坐标;
(2)求抛物线的解析式;
(3)求点P到点A的距离与点P到x轴的距离之差;
(4)当点P位于何处时,△APB的周长有最小值,并求出△APB的周长的最小值.
已知二次函数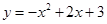 .
.
(1)求函数图像的顶点坐标,并画出这个函数的图像;
(2)根据图像,直接写出:
①当函数值y为正数时,自变量x的取值范围;
②当―2<x<2时,函数值y的取值范围.
如图1,对于平面上不大于 的∠MON,我们给出如下定义:若点P在∠MON的内部或边界上,作PE⊥OM于点E,PF⊥ON于点F,则称PE+PF为点P相对于∠MON的“点角距离”,记为
的∠MON,我们给出如下定义:若点P在∠MON的内部或边界上,作PE⊥OM于点E,PF⊥ON于点F,则称PE+PF为点P相对于∠MON的“点角距离”,记为 .
.
如图2,在平面直角坐标系xOy中,对于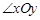 ,点P为第一象限内或两条坐标轴正半轴上的动点,且满足
,点P为第一象限内或两条坐标轴正半轴上的动点,且满足 5,点P运动形成的图形记为图形G.
5,点P运动形成的图形记为图形G.
(1)满足条件的其中一个点P的坐标是 ,图形G与坐标轴围成图形的面积等于 ;
(2)设图形G与x轴的公共点为点A,已知 ,
, ,求
,求 的值;
的值;
(3)如果抛物线 经过(2)中的A,B两点,点Q在A,B两点之间的抛物线上(点Q可与A,B两点重合),求当
经过(2)中的A,B两点,点Q在A,B两点之间的抛物线上(点Q可与A,B两点重合),求当 取最大值时,点Q 的坐标.
取最大值时,点Q 的坐标.
如图,在平面直角坐标系中,抛物线y=ax2+bx﹣3(a≠0)与x轴交于点A(﹣2,0)、B(4,0)两点,与y轴交于点C.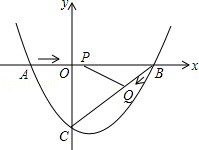
(1)求抛物线的解析式;
(2)点P从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时点Q从B点出发,在线段BC上以每秒1个单位长度的速度向C点运动,其中一个点到达终点时,另一个点也停止运动,当△PBQ存在时,求运动多少秒使△PBQ的面积最大,最大面积是多少?
(3)当△PBQ的面积最大时,在BC下方的抛物线上存在点K,使S△CBK:S△PBQ=5:2,求K点坐标.
已知点P(1,-2a)在二次函数y=ax2+6的图象上,并且点P关于x轴的对称点在反比例函数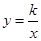 的图象上。
的图象上。
(1)求此二次函数和反比例函数的解析式;
(2)点(-1,4)是否同时在(1)中的两个函数图象上?
雅安地震牵动着全国人民的心,某单位开展了“一方有难,八方支援”赈灾捐款活动.第一天收到捐款10 000元,第三天收到捐款12 100元.
(1)如果第二天、第三天收到捐款的增长率相同,求捐款增长率;
(2)按照(1)中收到捐款的增长速度,第四天该单位能收到多少捐款?
已知平面直角坐标系中两定点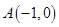 、
、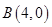 ,抛物线
,抛物线 过点A,B,与y交于C点,点P(m,n)为抛物线上一点.
过点A,B,与y交于C点,点P(m,n)为抛物线上一点.
(1)求抛物线的解析式和点C的坐标;
(2)当∠APB为钝角时,求m的取值范围;
(3)当∠PAB=∠ABC时,求点P的坐标.
已知二次函数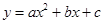 (a≠0),列表如下:
(a≠0),列表如下:
| x |
…… |
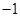 |
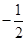 |
0 |
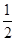 |
1 |
 |
2 |
… |
| y |
…… |
2 |
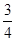 |
0 |
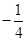 |
0 |
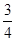 |
2 |
… … |
(1)根据表格所提供的数据,请你写出顶点坐标___________,对称轴__________。
(2)求出二次函数解析式。
(本小题满分10分)如图,抛物线 与
与 轴交
轴交 、
、 两点,直线
两点,直线 与抛物线交于A、C两点,其中C点的横坐标为2.
与抛物线交于A、C两点,其中C点的横坐标为2.
(1)求抛物线及直线AC的函数表达式;
(2)若P点是线段AC上的一个动点,过P点作 轴的平行线交抛物线于F点,求线段PF长度的最大值.
轴的平行线交抛物线于F点,求线段PF长度的最大值.
已知二次函数的顶点坐标为(2,-2),且其图象经过点(3,1),求此二次函数的解析式,并求出该函数图像与y轴的交点坐标。
如图,直线y=﹣x+3与x轴,y轴分别交于B,C两点,抛物线y=﹣x2+bx+c经过B,C两点,点A是抛物线与x轴的另一个交点.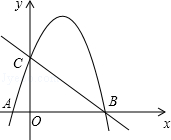
(1)求B、C两点坐标;
(2)求此抛物线的函数解析式;
(3)在抛物线上是否存在点P,使S△PAB=S△CAB,若存在,求出P点坐标,若不存在,请说明理由.
已知抛物线与x轴相交于A(-1,0),B(3,0)两点,顶点坐标为C(1,4),
(1)求该抛物线解析式,
(2)判断开口方向以及增减情况