动物园计划用长为120米的铁丝围成如图所示的兔笼,(不包括顶棚)供学习小组的同学参观,其中一面靠墙,(墙足够长)怎样设计围成的面积最大?
已知二次函数y=ax2+bx-3的图象经过点A(2,-3),B(-1,0). 求二次函数的解析式;
二次函数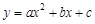 的图象与x轴交于点A(-1, 0),与y轴交于点C(0,-5),且经过点D(3,-8).
的图象与x轴交于点A(-1, 0),与y轴交于点C(0,-5),且经过点D(3,-8).
(1)求此二次函数的解析式和顶点坐标;
(2)请你写出一种平移的方法,使平移后抛物线的顶点落在原点处,并写出平移后抛物线的解析式.
已知抛物线y=x2+bx+c经过(2,-1)和(4,3)两点.
(1)求出这个抛物线的解析式;
(2)将该抛物线向右平移1个单位,再向下平移3个单位,得到的新抛物线解析式为 .
已知:已知二次函数 的图象对称轴为
的图象对称轴为 ,且过点B(-1,0).求此二次函数的表达式.
,且过点B(-1,0).求此二次函数的表达式.
已知二次函数y=-x2+bx+c的图象如图所示,求此二次函数的解析式和抛物线的顶点坐标.
已知:二次函数 的图象开口向上,并且经过原点
的图象开口向上,并且经过原点
 .
.
(1)求 的值;
的值;
(2)用配方法求出这个二次函数图象的顶点坐标.
如图,用长为20米的篱笆恰好围成一个扇形花坛,且扇形花坛的圆心角小于180°,设扇形花坛的半径为 米,面积为
米,面积为 平方米.(注:
平方米.(注: 的近似值取3)
的近似值取3)
(1)求出 与
与 的函数关系式,并写出自变量
的函数关系式,并写出自变量 的取值范围;
的取值范围;
(2)当半径 为何值时,扇形花坛的面积最大,并求面积的最大值.
为何值时,扇形花坛的面积最大,并求面积的最大值.
已知抛物线 的顶点在x轴上,且与y轴交于A点. 直线
的顶点在x轴上,且与y轴交于A点. 直线 经过A、B两点,点B的坐标为(3,4).
经过A、B两点,点B的坐标为(3,4).
(1)求抛物线的解析式,并判断点B是否在抛物线上;
(2)如果点B在抛物线上,P为线段AB上的一个动点(点P与A、B不重合),过P作x轴的垂线与这个二次函数的图象交于点E,设线段PE的长为h,点P的横坐标为x.当x为何值时,h取得最大值,求出这时的h值.
已知:二次函数y=x2-4x+3.
(1)将y=x2-4x+3化成 的形式;
的形式;
(2)求出该二次函数图象的对称轴和顶点坐标;
(3)当x取何值时,y<0.
如图,已知二次函数y=x2+bx+c过点A(1,0),C(0,﹣3).
(1)求此二次函数的解析式;
(2)在抛物线上存在一点P使△ABP的面积为10,请求出出点P的坐标.
二次函数的图象经过点 ,
, ,
, .
.
(1)求此二次函数的关系式;
(2)求此二次函数图象的顶点坐标;
(3)填空:把二次函数的图象沿坐标轴方向最少平移 个单位,使得该图象的顶点在原点.