[北京]2014届北京市燕山九年级上学期期末考试数学试卷

若2x=3y，则的值为（  ）

A．

B．

C．

D．

二次函数的最小值是（     ）

已知⊙O的半径为5，点P到圆心O的距离为7，那么点P与⊙O的位置关系是（  ）

在正方形网格中，△ABC的位置如图所示，则sinB的值是（      ）

A．

B．

C．

D．

如图，⊙O的直径AB=12，CD是⊙O的弦，CD⊥AB，垂足为P，且BP : AP="1" : 5.则CD的长为 （   ）

A．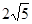

B．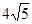

C．

D．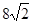

已知圆锥的底面半径为3cm，母线长为5cm，则此圆锥的侧面积为 (     )

如图，在Rt△ABC中，∠C=90°，P是斜边上一定点，过点P作直线与一直角边交于点Q使图中出现两个相似三角形，这样的点Q有 (    )

如图，⊙O上有两点A与P，且OA⊥OP，若A点固定不动，P点在圆上匀速运动一周，那么弦AP的长度与时间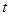的函数关系的图象可能是(       )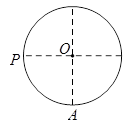


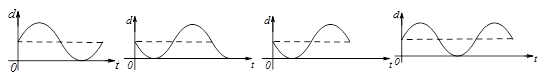
①               ②                    ③                         ④

如果两个相似三角形的相似比是2:3，那么它们的周长比是       ．

已知抛物线经过两点和，则与的大小关系是       ．

一个长方体木箱沿斜面下滑，当木箱滑至如图位置时，AB=m，已知木箱高BE=m，斜坡角为30°，则木箱端点E距地面AC的高度EF为       m．

我们把图（1）称作正六边形的基本图，将此基本图不断复制并平移，使得相邻两个基本图的一边重合，这样得到图（2），图（3），…，
如此进行下去，直至得图（n）．

图（1）        图（2）               图（3）
（1）将图（n）放在直角坐标系中，设其中第一个基本图的对称中心O₁的坐标为（x₁，4），则x₁=             ；
（2）图（n）的对称中心的横坐标为           

计算：2sin30°＋cos45°－tan60°．

已知抛物线y=x²+bx+c经过（2，－1）和（4,3）两点．
(1)求出这个抛物线的解析式；
(2)将该抛物线向右平移1个单位，再向下平移3个单位，得到的新抛物线解析式为             .

如图，在△ABC中，∠C=90°，cosA=，AC=9.求AB的长和tanB的值．

如图：四边形ABCD和四边形AEFC都是矩形，点B在EF边上.

（1）请你找出图中一对相似三角形（相似比不等于1），并加以证明；
（2）若四边形ABCD的面积为20，求四边形AEFC的面积．

如图，已知，，是平面直角坐标系中三点．

（1）请你画出ABC关于原点O对称的A₁B₁C₁；
（2）请写出点A关于y轴对称的点A₂的坐标．若将点A₂向上平移h个单位，使其落在A₁B₁C₁内部，指出h的取值范围.

如图，⊙O是RtABC的外接圆，∠ABC=90°，AC=13，BC=5，弦BD=BA，BE⊥DC交DC的延长线于点E．

（1）求证：∠BCA=∠BAD；
（2）求DE的长．

已知二次函数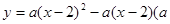为常数，且.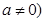
（1）求证：不论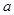为何值，该函数的图象与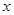轴总有两个公共点；
（2）设该函数的图象的顶点为C，与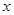轴交于A，B两点，当△ABC的面积等于2时，求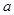的值.

如图，AB为⊙O的直径，点C在⊙O上，点P是直径AB上的一点，（不与A，B重合），过点P作AB的垂线交BC的延长线于点Q.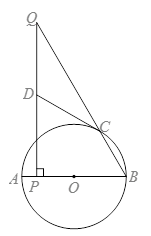

（1）点D在线段PQ上，且DQ=DC.求证：CD是⊙O的切线；
（2）若sinQ=，BP=6，AP=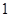，求QC的长.

在2014年“元旦”前夕，某商场试销一种成本为30元的文化衫，经试销发现，若每件按34元的价格销售，每天能卖出36件；若每件按39元的价格销售，每天能卖出21件．假定每天销售件数y（件）是销售价格x(元)的一次函数．
（1）直接写出y与x之间的函数关系式y=                      ．
（2）在不积压且不考虑其他因素的情况下，每件的销售价格定为多少元时，才能使每天获得的利润P最大？

已知四边形ABCD中，E，F分别是AB，AD边上的点，DE与CF交于点G．（1）如图1，若四边形ABCD是矩形，且DE⊥CF．则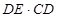       （填“<”或“=”或“>”）；
（2）如图2，若四边形ABCD是平行四边形，试探究：
当∠B与∠EGC满足什么关系时，使得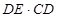=成立？并证明你的结论；
（3）如图3，若BA="BC=" 3，DA="DC=" 4，∠BAD= 90°，DE⊥CF．则的值为        ．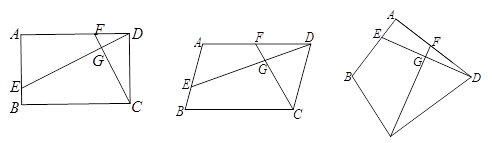

图1                     图2                     图3

已知抛物线与轴相交于，两点（点在点的左侧），与轴相交于点．

（1）点的坐标为        ，点的坐标为        ；
（2）在轴的正半轴上是否存在点，使以点，，为顶点的三角形与相似？若存在，求出点的坐标，若不存在，请说明理由．

定义：把一个半圆与抛物线的一部分合成封闭图形，我们把这个封闭图形称为“蛋圆”．如果一条直线与“蛋圆”只有一个交点，那么这条直线叫做“蛋圆”的切线．如图，A，B，C，D分别是“蛋圆”与坐标轴的交点，已知点D的坐标为（0,8），AB为半圆的直径，半圆的圆心M的坐标为（1,0），半圆半径为3．

（1）请你直接写出“蛋圆”抛物线部分的解析式          ，自变量的取值范围是          ；
（2）请你求出过点C的“蛋圆”切线与x轴的交点坐标；
（3）求经过点D的“蛋圆”切线的解析式．