[北京]2014届北京市东城区初三第一学期期末统一测试数学试卷
袋子中装有4个黑球和2个白球,这些球的形状、大小、质地等完全相同,在看不到球的条件下,随机地从袋子中摸出三个球.下列是必然事件的是
| A.摸出的三个球中至少有一个球是黑球 |
| B.摸出的三个球中至少有一个球是白球 |
| C.摸出的三个球中至少有两个球是黑球 |
| D.摸出的三个球中至少有两个球是白球 |
如图,已知⊙O是△ABD的外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=58°,则∠BCD等于
| A.116° | B.64° | C.58° | D.32° |
如图,电线杆上的路灯距离地面8米,身高1.6米的小明(AB)站在距离电线杆的底部(点O)20米的A处, 则小明的影子AM长为
A.4米 B.5米
C.6米 D.8米
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是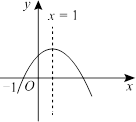
| A.a>0 |
| B.当-1<x<3时,y>0 |
| C.c<0 |
| D.当x≥1时,y随x的增大而增大 |
如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是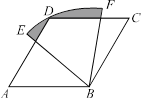
A.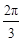 - -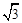 |
B.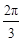 - -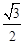 |
C.π-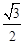 |
D.π-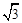 |
如图,正方形ABCD中,AB=8cm,对角线AC,BD相交于点O,点E,F分别从B,C两点同时出发,以1cm/s的速度沿BC,CD运动,到点C,D时停止运动.设运动时间为t(s),△OEF的面积为S(cm2),则S(cm2)与t(s)的函数关系可用图象表示为( )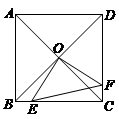
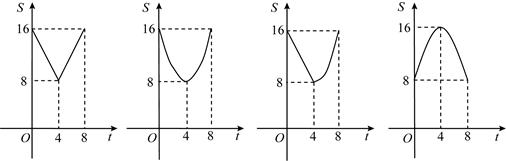
A. B. C. D.
如图,在Rt△OAB中,∠B=90°∠AOB=30°,将△OAB绕点O逆时针旋转100°得到△OA1B1,则∠A1OB= °
射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,QM=4cm.动点P从点Q出发,沿射线QN以每秒1cm的速度向右移动,经过t秒,以点P为圆心,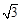 cm为半径的圆与△
cm为半径的圆与△ 的边相切,请写出t可取的所有值 .
的边相切,请写出t可取的所有值 .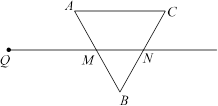
如图,△ABC和△A’B’C’是两个完全重合的直角三角板,∠B=∠B’=30º,斜边长为10cm.三角形板A’B’C’绕直角顶点C顺时针旋转,当点A'落在AB边上时,求C’A’旋转所构成的扇形的弧长 .
.

如图,在平行四边形ABCD中,E为CD上一点,连结AE,BD,且AE,BD交于点F,S△DEF∶S△ABF=4∶25,求DE∶EC的值.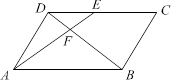
二次函数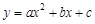 的图象与x轴交于点A(-1, 0),与y轴交于点C(0,-5),且经过点D(3,-8).
的图象与x轴交于点A(-1, 0),与y轴交于点C(0,-5),且经过点D(3,-8).
(1)求此二次函数的解析式和顶点坐标;
(2)请你写出一种平移的方法,使平移后抛物线的顶点落在原点处,并写出平移后抛物线的解析式.
画图:
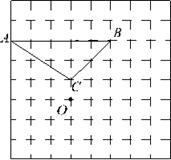
(1)如图,已知△ABC和点O.将△ABC绕点O顺时针旋转90°得到△A1B1C1,在网格中画出△A1B1C1;
(2)如图,AB是半圆的直径,图1中,点C在半圆外;图2中,点C在半圆内,请仅用无刻度的直尺(只能画线)按要求画图.
(ⅰ)在图1中,画出△ABC的三条高的交点;
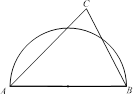
(ⅱ)在图2中,画出△ABC中AB边上的高.
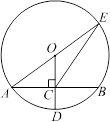
如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,求EC的长.
如图,有四张背面相同的纸牌A,B,C,D,其正面分别是红桃、方块、黑桃、梅花,其中红桃、方块为红色,黑桃、梅花为黑色.小明将这4张纸牌背面朝上洗匀后,摸出一张,将剩余3张洗匀后再摸出一张.请用画树状图或列表的方法求摸出的两张牌均为黑色的概率.
在一幅长8分米,宽6分米的矩形风景画(如图①)的四周镶宽度相同的金色纸边,制成一幅矩形挂图(如图②).如果要使整个挂图的面积是80平方分米,求金色纸边的宽.
在Rt△ACB中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC,AB分别交于点D,E,且∠CBD=∠A.
(1)判断直线BD与⊙O的位置关系,并证明你的结论;
(2)若AD∶AO=8∶5,BC=3,求BD的长.
阅读理解:
如图1,若在四边形ABCD的边AB上任取一点E(点E与点A,B不重合),分别连结ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.解决问题:
(1)如图1,若∠A=∠B=∠DEC=55°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图2,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图2中画出矩形ABCD的边AB上的一个强相似点E;
拓展探究:
(3)如图3,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处.若点E恰好是四边形ABCM的边AB上的一个强相似点,请直接写出 的值.
的值.

图1 图2 图3
已知二次函数y=a(x-m)2-2a(x-m)(a,m为常数,且a≠0).
(1)求证:不论a与m为何值,该函数的图象与x轴总有两个公共点;
(2)设该函数的图象的顶点为C,与x轴交于A,B两点,当△ABC是等腰直角三角形时,求a的值.
如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90º,∠B=∠E=30º.
(1)操作发现
如图2,固定△ABC,使△DEC绕点C顺时针旋转.当点D恰好落在AB边上时,填空:

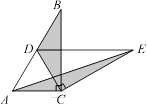
线段DE与AC的位置关系是 ;
设△BDC的面积为S1,△AEC的面积为S2,则S1与S2的数量关系是 ,证明你的结论;
猜想论证
当△DEC绕点C旋转到图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AE中BC,CE边上的高,请你证明小明的猜想.





 粤公网安备 44130202000953号
粤公网安备 44130202000953号