[北京]2014届北京市海淀区九年级第一学期期末考试数学试卷
如图,将一张矩形纸片沿对角线剪开得到两个直角三角形纸片,将这两个直角三角形纸片通过图形变换构成以下四个图形,这四个图形中是中心对称图形的是( )
A. B. C. D.
如图,在△ 中,点
中,点 、
、 分别为边
分别为边 、
、 上的点,且
上的点,且 ∥
∥ ,若
,若 ,
,  ,
,  ,则
,则 的长为( )
的长为( )
| A.3 | B.6 | C.9 | D.12 |
二次函数 的图象如图所示,将其绕坐标原点O旋转
的图象如图所示,将其绕坐标原点O旋转 ,则旋转后的抛物线的解析式为( )
,则旋转后的抛物线的解析式为( )
A. |
B. |
C. |
D. |
在平面直角坐标系 中,以点
中,以点 为圆心,4为半径的圆与y轴所在直线的位置关系是( )
为圆心,4为半径的圆与y轴所在直线的位置关系是( )
| A.相离 | B.相切 | C.相交 | D.无法确定 |
如图, 是⊙
是⊙ 的切线,
的切线,  为切点,
为切点, 的延长线交⊙
的延长线交⊙ 于
于 点,连接
点,连接 ,若
,若 ,
, ,则
,则 等于( )
等于( ) 
| A.4 | B.6 | C. |
D. |
如图,Rt△ABC中,AC=BC=2,正方形CDEF的顶点D、F分别在AC、BC边上, C、D两点不重合,设CD的长度为x,△ABC与正方形CDEF重叠部分的面积为y,则下列图象中能表示y与x之间的函数关系的是( )




A. B. C. D.
已知点P(-1,m)在二次函数 的图象上,则m的值为 ;平移此二次函数的图象,使点P与坐标原点重合,则平移后的函数图象所对应的解析式为 .
的图象上,则m的值为 ;平移此二次函数的图象,使点P与坐标原点重合,则平移后的函数图象所对应的解析式为 .
在△ 中,
中, 分别是
分别是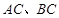 边上的点,
边上的点, 是
是 边的
边的 等分点,
等分点,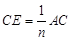 ,
, .如图1,若
.如图1,若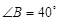 ,
, ,则∠
,则∠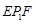 +∠
+∠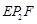 +∠
+∠ +
+ 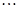 +∠
+∠ 度;如图2,若
度;如图2,若 ,
, ,则∠
,则∠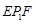 +∠
+∠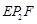 +∠
+∠ +
+ 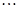 +∠
+∠ (用含
(用含 ,
, 的式子表示).
的式子表示).
如图,用长为20米的篱笆恰好围成一个扇形花坛,且扇形花坛的圆心角小于180°,设扇形花坛的半径为 米,面积为
米,面积为 平方米.(注:
平方米.(注: 的近似值取3)
的近似值取3)
(1)求出 与
与 的函数关系式,并写出自变量
的函数关系式,并写出自变量 的取值范围;
的取值范围;
(2)当半径 为何值时,扇形花坛的面积最大,并求面积的最大值.
为何值时,扇形花坛的面积最大,并求面积的最大值.
如图,AB为 O的直径,射线AP交
O的直径,射线AP交 O于C点,∠PCO的平分线交
O于C点,∠PCO的平分线交 O于D点,过点D作
O于D点,过点D作 交AP于E点.
交AP于E点.
(1)求证:DE为 O的切线;
O的切线;
(2)若 ,
, ,求直径
,求直径 的长.
的长.
已知二次函数 .
.
(1)若点 与
与 在此二次函数的图象上,则
在此二次函数的图象上,则
 (填 “>”、“=”或“<”);
(填 “>”、“=”或“<”);
(2)如图,此二次函数的图象经过点 ,正方形ABCD的顶点C、D在x轴上, A、B恰好在二次函数的图象上,求图中阴影部分的面积之和.
,正方形ABCD的顶点C、D在x轴上, A、B恰好在二次函数的图象上,求图中阴影部分的面积之和.
晓东在解一元二次方程时,发现有这样一种解法:
如:解方程 .
.
解:原方程可变形,得 .
. ,
, ,
, .
.
直接开平方并整理,得 .
.
我们称晓东这种解法为“平均数法”.
(1)下面是晓东用“平均数法”解方程 时写的解题过程.
时写的解题过程.
解:原方程可变形,得 .
. ,
, .
.
直接开平方并整理,得  ¤.
¤.
上述过程中的“ ”,“
”,“ ” ,“☆”,“¤”表示的数分别为_____,_____,_____,_____.
” ,“☆”,“¤”表示的数分别为_____,_____,_____,_____.
(2)请用“平均数法”解方程: .
.
已知抛物线 (
( ).
).
(1)求抛物线与 轴的交点坐标;
轴的交点坐标;
(2)若抛物线与 轴的两个交点之间的距离为2,求
轴的两个交点之间的距离为2,求 的值;
的值;
(3)若一次函数 的图象与抛物线始终只有一个公共点,求一次函数的解析式.
的图象与抛物线始终只有一个公共点,求一次函数的解析式.
已知四边形ABCD和四边形CEFG都是正方形 ,且AB>CE.
(1)如图1,连接BG、DE.求证:BG=DE;
(2)如图2,如果正方形ABCD的边长为 ,将正方形CEFG绕着点C旋转到某一位置时恰好使得CG//BD,BG=BD.
,将正方形CEFG绕着点C旋转到某一位置时恰好使得CG//BD,BG=BD.
①求 的度数;
的度数;
②请直接写出正方形CEFG的边长的值.
 的值是( )
的值是( )
 的方程
的方程 没有实数根,则
没有实数根,则 的取值范围是
的取值范围是




 (填 “>”、“=”或“<”).
(填 “>”、“=”或“<”). 是⊙O上的点,若
是⊙O上的点,若 ,则
,则 ___________度.
___________度.
 .
. .
. 和△
和△ 中,
中, ,
, 为线段
为线段 上一点,且
上一点,且 .
. .
.
 经过(0,-1),(3,2)两点.求它的解析式及顶点坐标.
经过(0,-1),(3,2)两点.求它的解析式及顶点坐标. ∥
∥ 且
且 ,E是BC上一点,且
,E是BC上一点,且 .求证:
.求证: .
.
 的方程
的方程  有实数根.
有实数根.  的取值范围;
的取值范围; 的图象与x轴交于A、B两点(B在A的左侧),顶点为C, 点D(1,m)在此二次函数图象的对称轴上,过点D作y轴的垂线,交对称轴右侧的抛物线于E点.
的图象与x轴交于A、B两点(B在A的左侧),顶点为C, 点D(1,m)在此二次函数图象的对称轴上,过点D作y轴的垂线,交对称轴右侧的抛物线于E点.
 .求证:
.求证: ;
; 粤公网安备 44130202000953号
粤公网安备 44130202000953号