已知四边形ABCD和四边形CEFG都是正方形 ,且AB>CE.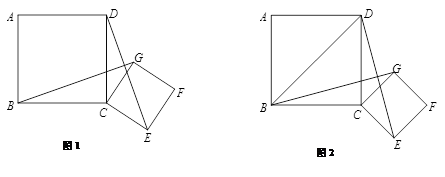
(1)如图1,连接BG、DE.求证:BG=DE;
(2)如图2,如果正方形ABCD的边长为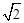 ,将正方形CEFG绕着点C旋转到某一位置时恰好使得CG//BD,BG=BD.
,将正方形CEFG绕着点C旋转到某一位置时恰好使得CG//BD,BG=BD.
①求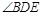 的度数;
的度数;
②请直接写出正方形CEFG的边长的值.
相关知识点
推荐套卷
已知四边形ABCD和四边形CEFG都是正方形 ,且AB>CE.
(1)如图1,连接BG、DE.求证:BG=DE;
(2)如图2,如果正方形ABCD的边长为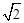 ,将正方形CEFG绕着点C旋转到某一位置时恰好使得CG//BD,BG=BD.
,将正方形CEFG绕着点C旋转到某一位置时恰好使得CG//BD,BG=BD.
①求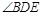 的度数;
的度数;
②请直接写出正方形CEFG的边长的值.