某校为了满足学生借阅图书的需求，计划购买一批新书，为此可，该校图书管理员对一周内本校学生从图书馆借出各类图书的数量进行了统计，结果如下图.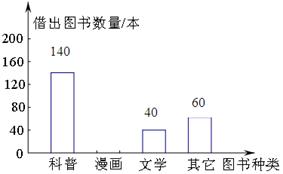
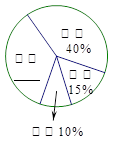
请你根据统计图中的信息，解答下列问题：
（1）补全条形统计图和扇形统计图；
（2）该校学生最喜欢借阅哪类图书？
（3）该校计划购买新书600本，若按扇形统计图中的百分比来相应地确定漫画、科普、文学、其他这四类图书的购买量，求应购买这四类图书各多少本？
下面是近年来国内生产总值年增长率的变化统计表：
| 年份 |
1994 |
1995 |
1996 |
1997 |
1998 |
1999 |
2000 |
| 生产总值年增长率(%) |
12.6 |
105 |
9.6 |
8.8 |
7.8 |
7.1 |
8.0 |
（1）用一幅折线统计图表示国内生产总值年增长率的变化情况；
（2）将上面的数据制成形象生动的统计图；
（3）如果要利用面积分别表示五年的生产总值年增长率，t年的生产总值年增长率的面积之比大约是多少？
（4）哪一年国内生产总值的年增长率开始回升？
小李通过对某地区1998～2000年快餐公司发展情况的调查，制成了该地区快餐公司个数情况的条形图（如图1）和快餐公司盒饭年销量的平均情况条形图（如图2）,利用这两张图表共同提供的信息，解答下列问题：
（1）1999年该地区销售盒饭共______________万盒；
（2）该地区盒饭销量最大的年份是__________年，这一年的年销量是________万盒；
（3）这三年中该地区每年平均销售盒饭多少万盒？
某校初一年级篮球队12名同学的身高（cm）分别如下：
171，168，170，173，165，178，166，161，176，172，164，165
求全队同学的平均身高。（精确到1cm）
下面是在博物馆里的一段对话管理员：
小姐，这个化石有800 002年了。
参观者：你怎么知道得这么精确？
管理员：两年前，有个考古学家参观过这里，他说这个化石有80万年了，现在，两年过去了，所以是800 002年。管理员的推断对吗？为什么？
粤公网安备 44130202000953号