晓东在解一元二次方程时,发现有这样一种解法：
如：解方程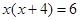
．
解：原方程可变形,得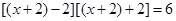
.
,
,
.
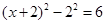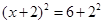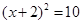直接开平方并整理,得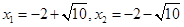
．
我们称晓东这种解法为“平均数法”.
（1）下面是晓东用“平均数法”解方程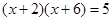
时写的解题过程．
解：原方程可变形,得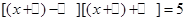
.
,
.
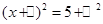直接开平方并整理,得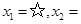 
¤．
上述过程中的“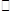
”,“
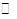” ,“☆”,“¤”表示的数分别为_____,_____,_____,_____．
（2）请用“平均数法”解方程：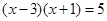
．
.
、
在第一象限的图像，
，过
，作
轴的平行线交
，交
轴于
，若
；求双曲线
中，
． 
＞
．
．相关知识点
推荐套卷
晓东在解一元二次方程时,发现有这样一种解法：
如：解方程．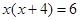
解：原方程可变形,得.,,.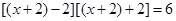
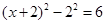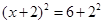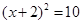直接开平方并整理,得．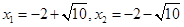
我们称晓东这种解法为“平均数法”.
（1）下面是晓东用“平均数法”解方程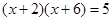时写的解题过程．
解：原方程可变形,得.,.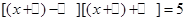
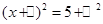直接开平方并整理,得 ¤．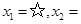
上述过程中的“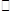”,“”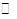 ,“☆”,“¤”表示的数分别为_____,_____,_____,_____．
（2）请用“平均数法”解方程：．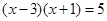
粤公网安备 44130202000953号