如图,在平面直角坐标系中,已知点A(0,1)、B(3,5),以AB为边作如图所示的正方形ABCD,顶点在坐标原点的抛物线恰好经过点D,P为抛物线上的一动点.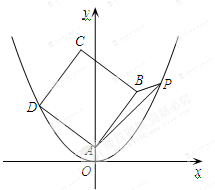
(1)直接写出点D的坐标;
(2)求抛物线的解析式;
(3)求点P到点A的距离与点P到x轴的距离之差;
(4)当点P位于何处时,△APB的周长有最小值,并求出△APB的周长的最小值.
相关知识点
推荐套卷
如图,在平面直角坐标系中,已知点A(0,1)、B(3,5),以AB为边作如图所示的正方形ABCD,顶点在坐标原点的抛物线恰好经过点D,P为抛物线上的一动点.
(1)直接写出点D的坐标;
(2)求抛物线的解析式;
(3)求点P到点A的距离与点P到x轴的距离之差;
(4)当点P位于何处时,△APB的周长有最小值,并求出△APB的周长的最小值.