已知抛物线抛物线y n=-(x-an)2+an(n为正整数,且0<a1<a2<…<an)与x轴的交点为An-1(bn-1,0)和An(bn,0),当n=1时,第1条抛物线y1=-(x-a1)2+a1与x轴的交点为A0(0,0)和A1(b1,0),其他依此类推.
(1)求a1,b1的值及抛物线y2的解析式;
(2)抛物线y3的顶点坐标为( , );
依此类推第n条抛物线yn的顶点坐标为( , );
所有抛物线的顶点坐标满足的函数关系是 ;
(3)探究下列结论:
若用An-1An表示第n条抛物线被x轴截得得线段长,直接写出A0A1的值,并求出An-1An;
相关知识点
推荐套卷
 的顶点
的顶点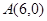 ,
, ,
,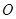 是坐标原点.将
是坐标原点.将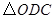 .
.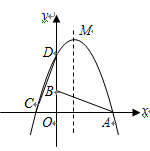
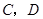 两点的坐标;
两点的坐标;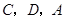 三点的抛物线的解析式,并求此抛物线的顶点
三点的抛物线的解析式,并求此抛物线的顶点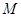 的坐标;
的坐标;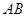 上是否存在点
上是否存在点 使得
使得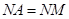 ?若存在,请求出点
?若存在,请求出点 ,AD是△ABC的高,AE是△ABC的外接圆⊙O的直径,
,AD是△ABC的高,AE是△ABC的外接圆⊙O的直径,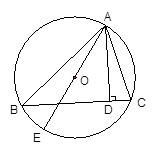
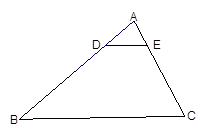
 cm, 弓形的高为6cm.
cm, 弓形的高为6cm.



 粤公网安备 44130202000953号
粤公网安备 44130202000953号