初中数学二次函数在给定区间上的最值试题

将一条长为20cm的铁丝剪成两段，并以每一段铁丝的长度为周长各做成一个正方形，则这两个正方形面积之和的最小值是             cm²．

如图，在平面直角坐标系中，直线与抛物线交于A、B两点，点A在x轴上，点B的横坐标为－8．

（1）求该抛物线的解析式；
（2）点P是直线AB上方的抛物线上一动点（不与点A、B重合），过点P作x轴的垂线，垂足为C，交直线AB于点D，作PE⊥AB于点E．
①设△PDE的周长为，点P的横坐标为，求关于的函数关系式，并求出的最大值；
②连接PA，以PA为边作图示一侧的正方形APFG．随着点P的运动，正方形的大小、位置也随之改变．当顶点F或G恰好落在轴上时，求出对应点P的坐标．

已知二次函数图象的顶点在原点O，经过点A（1，）；点F（0，1）在y轴上．直线y=﹣1与y轴交于点H．

（1）求二次函数的解析式；
（2）点P是（1）中图象上的点，过点P作x轴的垂线与直线y=﹣1交于点M，求证：FM平分∠OFP；
（3）当△FPM是等腰直角三角形时，求P点的坐标．

如图，平面直角坐标系中，为坐标原点，抛物线交x轴于A、B两点（点A在点B的左侧），交y轴于点C，以OB、OC为边作矩形OBDC，CD交抛物线于G．

（1）求OB和OC的长；
（2）抛物线的对称轴在边OB（不包括O、B两点）上作平行移动，交x轴于点E，交CD于点F，交BC于点M，交抛物线于点P．设OE＝m，PM＝h，求h与m的函数关系式，并求PM的最大值；
（3）连接PC，在CD上方的抛物线部分是否存在这样的点P，使得以P、C、F为顶点的三角形与△BEM相似？若存在，求出相应的m的值，并判断△PCM的形状；若不存在，请说明理由．

某宾馆客房部有60个房间供游客居住，当每个房间的定价为每天200元时，房间可以住满．当每个房间每天的定价每增加10元时，就会有一个房间空闲．对有游客入住的房间，宾馆需对每个房间每天支出20元的各种费用．
设每个房间每天的定价增加x元．求：
（1）房间每天的入住量y（间）关于x（元）的函数关系式；
（2）该宾馆每天的房间收费z（元）关于x（元）的函数关系式；
（3）该宾馆客房部每天的利润w（元）关于x（元）的函数关系式；当每个房间的定价为每天多少元时，w有最大值？最大值是多少？

如图，在平面直角坐标系xoy中，直线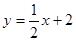与x 轴交于点A，与y轴交于点C．抛物线y=ax²+bx+c的对称轴是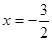且经过A、C两点，与x轴的另一交点为点B．  

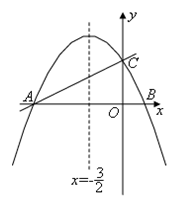
（1）①直接写出点B的坐标；②求抛物线解析式．
（2）若点P为直线AC上方的抛物线上的一点，连接PA，PC．求△PAC的面积的最大值，并求出此时点P的坐标；
（3）抛物线上是否存在点M，过点M作MN垂直x轴于点N，使得以点A、M、N为顶点的三角形与△ABC相似？若存在，求出点M的坐标；若不存在，请说明理由．

某一型号飞机着陆后滑行的距离y（单位：m）与滑行时间x（单位：s）之间的函数表达式是y = 60x－1．5x²，该型号飞机着陆后需滑行       m才能停下来．

在“母亲节”期间，某校部分团员参加社会公益活动，准备购进一批许愿瓶进行销售，并将所得利润捐助给慈善机构．根据市场调查，这种许愿瓶一段时间内的销售量 （单位：个）与销售单价 （单位：元/个）之间的对应关系如图所示：

（1）与之间的函数关系是                     ．
（2）若许愿瓶的进价为6元/个，按照上述市场调查的销售规律，求销售利润 （单位：元）与销售单价 （单位：元/个）之间的函数关系式；
（3）若许愿瓶的进货成本不超过900元，要想获得最大利润，试确定这种许愿瓶的销售单价，并求出此时的最大利润．

如图，直线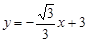与x轴、y轴分别交于B、C两点，经过B、C两点的抛物线与x轴交于另一点A，线段BC与抛物线的对称轴l相交于点D，设抛物线的顶点为P，连接AD，线段AD与y轴相交于点E．

（1）求该抛物线的解析式及对称轴；
（2）连结AP，请在y轴正半轴上找一点Q，使Q、C、D为顶点的三角形与△ADP全等，并求出点Q的坐标．将∠CED绕点E顺时针旋转，边EC旋转后与线段BC相交于点M，边ED旋转后与对称轴l相交于点N，若2DM=DN，求点M的坐标．

定义一种变换：平移抛物线F₁得到抛物线F₂，使F₂经过F₁的顶点A．设F₂的对称轴分别交F₁，F₂于点D，B，点C是点A关于直线BD的对称点．

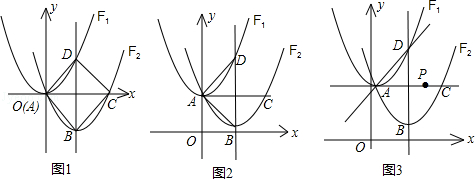
（1）如图1，若F₁：y=x²，经过变换后，得到F₂：y=x²+bx，点C的坐标为（2，0），则：
①b的值等于      ；
②四边形ABCD为（ ）
A、平行四边形；B、矩形；C、菱形；D、正方形．
（2）如图2，若F₁：y=ax²+c，经过变换后，点B的坐标为（2，c﹣1），求△ABD的面积；
（3）如图3，若F₁：y=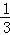x²﹣x+，经过变换后，AC=2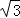，点P是直线AC上的动点，求点P到点D的距离和到直线AD的距离之和的最小值．

已知抛物线y=ax²+2x+c与x轴交于A（1，0）和点B，与y轴交于点C（0，﹣3）．
（1）求抛物线的解析式．
（2）如图1，已知点H的坐标为（0，1），设点M为y轴左侧抛物线上的一个动点，试猜想：是否存在这样的点M，使|MA﹣MH|的值最大，如果存在，请求出点M的坐标；如果不存在，请说明理由．
（3）如图2，过x轴上点E（﹣2，0）作ED⊥AB交抛物线于点D，在y轴上找一点F，使△EDF的周长最小，求出此时点F的坐标；
（4）如图3，已知点N（0，﹣1）．问在抛物线上是否存在点Q（点Q在y轴的左侧），使得△QNC的面积与△QNA的面积相等？若存在，求出点Q的坐标；若不存在，请说明理由．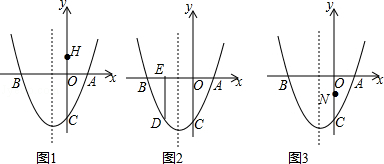

如图，在平面直角坐标系中，抛物线与x轴交于A、D两点，与y轴交于点B，四边形OBCD是矩形，点A的坐标为（1，0），点B的坐标为（0，4），已知点E（m，0）是线段DO上的动点，过点E作PE⊥x轴交抛物线于点P，交BC于点G，交BD于点H．

（1）求该抛物线的解析式；
（2）当点P在直线BC上方时，请用含m的代数式表示PG的长度；
（3）在（2）的条件下，是否存在这样的点P，使得以P、B、G为顶点的三角形与△DEH相似？若存在，求出此时m的值；若不存在，请说明理由．

“双十一”淘宝网销售一款工艺品，每件的成本是50元．销售期间发现：销售单价是100元时，每天的销售量是50件，而销售单价每降低1元，每天就可多售出5件．但要求销售单价不得低于成本．设当销售单价为x元时，每天的销售利润为y元．
（1）求出y与x之间的函数表达式；
（2）求出销售单价为多少元时，每天的销售利润最大？最大利润是多少？
（3）如果每天的销售利润不低于4000元，那么每天的总成本至少需要             元．
（每天的总成本=每件的成本×每天的销售量）

如图，已知抛物线的顶点坐标为M（1,4），且经过点N（2,3），与x轴交于A、B两点（点A在点B左侧），与y轴交于点C。

（1）点A、B、C的坐标分别为        、        、        。
（2）若直线y=kx+t经过C、M两点，且与x轴交于点D，试证明四边形CDAN是平行四边形；
（3）点P在抛物线的对称轴x=1上运动，请探索：在x轴上方是否存在这样的P点，使以P为圆心的圆经过A、B两点，并且与直线CD相切，若存在，请求出点P的坐标；若不存在，请说明理由。

二次函数的图象经过点（﹣1，4），且与直线相交于A、B两点（如图），A点在y轴上，过点B作BC⊥x轴，垂足为点C（﹣3，0）．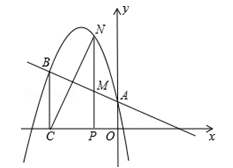

（1）求二次函数的表达式；
（2）点N是二次函数图象上一点（点N在AB上方），过N作NP⊥x轴，垂足为点P，交AB于点M，求MN的最大值；