某公司经销一种绿茶,每千克成本为50元.市场调查发现,在一段时间内,销售量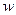 (千克)随销售单价
(千克)随销售单价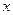 (元/千克)的变化而变化,具体关系式为:
(元/千克)的变化而变化,具体关系式为: ,且物价部门规定这种绿茶的销售单价不得高于90元/千克.设这种绿茶在这段时间内的销售利润为
,且物价部门规定这种绿茶的销售单价不得高于90元/千克.设这种绿茶在这段时间内的销售利润为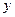 (元),解答下列问题:
(元),解答下列问题:
(1)求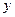 与
与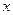 的关系式;
的关系式;
(2)当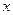 取何值时,
取何值时,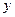 的值最大?
的值最大?
(3)如果公司想要在这段时间内获得2250元的销售利润,销售单价应定为多少元?
如图,点A,B的坐标分别为(1, 4)和(4, 4),抛物线 的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为
的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为 ,则点D的横坐标最大值为 .
,则点D的横坐标最大值为 . 
二次函数 的图象与
的图象与 轴交于
轴交于 、
、 两点,与
两点,与 轴相交于点
轴相交于点 .下列说法中,错误的是
.下列说法中,错误的是
A. 是等腰三角形 是等腰三角形 |
B.点 的坐标是 的坐标是 |
C. 的长为2 的长为2 |
D. 随 随 的增大而减小 的增大而减小 |
已知二次函数 的图象如图所示,它与x轴的一个交点的坐标为(-1,0),与y轴的交点坐标为(0,-3).
的图象如图所示,它与x轴的一个交点的坐标为(-1,0),与y轴的交点坐标为(0,-3).
(1)求此二次函数的解析式;
(2)求此二次函数的图象与x轴的另一个交点的坐标;
(3)根据图象回答:当x取何值时,y<0?
已知二次函数 .
.
(1)将 化成y ="a" (x - h) 2 + k的形式;
化成y ="a" (x - h) 2 + k的形式;
(2)指出该二次函数图象的对称轴和顶点坐标;
(3)当x取何值时,y随x的增大而增大?
将抛物线 先向左平移2个单位,再向下平移1个单位后得到新的抛物线,则新抛物线的解析式是
先向左平移2个单位,再向下平移1个单位后得到新的抛物线,则新抛物线的解析式是
A. |
B. |
C. |
D. |
已知:二次函数 的图象经过点
的图象经过点 和点
和点 .
.
(1)求该二次函数的解析式;
(2)将该二次函数图象向左平移几个单位,可使平移后所得图象经过坐标原点?并直接写出平移后所得图象与 轴的另一个交点的坐标.
轴的另一个交点的坐标.
已知:抛物线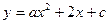 ,对称轴为直线
,对称轴为直线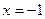 ,抛物线与y轴交于点
,抛物线与y轴交于点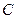 ,与
,与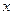 轴交于
轴交于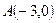 、
、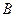 两点.
两点.
(1)求直线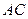 的解析式;
的解析式;
(2)若点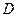 是线段
是线段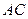 下方抛物线上的动点,求四边形
下方抛物线上的动点,求四边形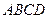 面积的最大值;
面积的最大值;
(3)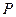 为抛物线上一点,若以线段
为抛物线上一点,若以线段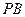 为直径的圆与直线
为直径的圆与直线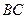 切于点
切于点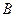 ,求点
,求点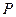 的坐标.
的坐标.
已知:关于x的一元二次方程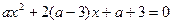 有两个实数根,且
有两个实数根,且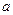 为非负整数.
为非负整数.
(1)求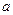 的值;
的值;
(2)若抛物线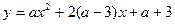 向下平移
向下平移 个单位后过点
个单位后过点 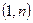 和点
和点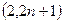 ,求
,求 的值;
的值;
(3)若抛物线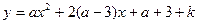 上存在两个不同的点
上存在两个不同的点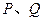 关于原点对称,求
关于原点对称,求 的取值范围.
的取值范围.
已知抛物线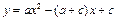 (其中a ≠ c且a ≠0).
(其中a ≠ c且a ≠0).
(1)求此抛物线与x轴的交点坐标;(用a,c的代数式表示)
(2)若经过此抛物线顶点A的直线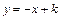 与此抛物线的另一个交点为
与此抛物线的另一个交点为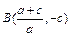 ,
,
求此抛物线的解析式;
(3)点P在(2)中x轴上方的抛物线上,直线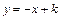 与 y轴的交点为C,若
与 y轴的交点为C,若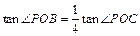 ,求点P的坐标;
,求点P的坐标;
(4)若(2)中的二次函数的自变量x在n≤x<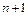 (n为正整数)的范围内取值时,记它的整数函数值的个数为N, 则N关于n的函数关系式为 .
(n为正整数)的范围内取值时,记它的整数函数值的个数为N, 则N关于n的函数关系式为 .
请阅读下面材料:
若 ,
, 是抛物线
是抛物线 (a ≠ 0)上不同的两点,证明直线
(a ≠ 0)上不同的两点,证明直线 为此抛物线的对称轴.
为此抛物线的对称轴.
有一种方法证明如下:
|
证明:∵ ,
, 是抛物线
是抛物线 (a ≠ 0)上不同的两点,
(a ≠ 0)上不同的两点,
 且
且
 ≠
≠
 .
.
 .
.
 .
.
 .
.
 (a ≠ 0)的对称轴为
(a ≠ 0)的对称轴为
 ,
,
 为此抛物线的对称轴.
为此抛物线的对称轴.
 ,
,
 是抛物线
是抛物线
 (a ≠ 0)上不同的两点,直线
(a ≠ 0)上不同的两点,直线
 为该抛物线的对称轴,那么自变量取
为该抛物线的对称轴,那么自变量取
 ,
,
 时函数值相等吗?写出你的猜想,并参考上述方法写出证明过程;
时函数值相等吗?写出你的猜想,并参考上述方法写出证明过程;
 当x = 4 时的函数值与x = 2007 时的函数值相等,求x = 2012时的函数值.
当x = 4 时的函数值与x = 2007 时的函数值相等,求x = 2012时的函数值.